“The artist is the creator of beautiful things.
To reveal art and conceal the artist is art’s aim.
Those who find ugly meanings in beautiful things are corrupt without being charming. This is a fault.
Those who find beautiful meanings in beautiful things are the cultivated. For these there is hope.
They are the elect to whom beautiful things mean only Beauty.”
Oscar Wilde [1]
Introduzione
Gli scacchi sono un universo entro cui ogni giocatore può vedere aspetti diversi del gioco e individuare varie tematiche. Nonostante gli scacchi abbiano come base una struttura competitiva (guerresca), è possibile anche intravedere un aspetto estetico/meditativo e notare come il gioco abbia mantenuto inalterato nei secoli il suo simbolismo e una specifica funzione di trasmettere messaggi e sviluppare capacità mentali. Gli scacchi sono diventati nell’arco del tempo una metafora adattabile a campi molto diversi per illustrare idee astratte e sistemi complessi oltre che un efficace strumento utilizzato da psicologi e scienziati cognitivi per comprendere meglio l’animo e la mente umana.
“Ho sempre amato la complessità – ha detto Marcel Duchamp1 – e con gli scacchi si possono creare problemi magnifici”. Questa frase dell’artista francese potrebbe essere il motto di artisti e intellettuali del XX [XXI] secolo, ossia di coloro che si sono incaricati di interpretare la complessa trama sottesa alla contemporaneità per trarne, in modi diversi, verità e bellezza. Nel XX secolo gli scacchi sono stati applicati alla soluzione di difficili problemi e sono stati oggetto di ammirazione e critica sotto il profilo estetico. Chiaramente la vibrante frase del pittore e scacchista francese sui “problemi magnifici” non si riferisce tanto alla bellezza fisica della scacchiera o dei suoi pezzi (come ci propongono gli antiquari), ma alla dinamica stessa del gioco, alla sua tensione sottesa e ai suoi imprevedibili risultati. Duchamp ha inoltre dichiarato che “I pezzi degli scacchi sono le lettere dell’alfabeto con cui si formano i pensieri che, mentre fanno un disegno visibile sulla scacchiera, esprimono la loro bellezza in modo astratto, come in un poema” [2].
Tutto questo mi ha indotto a considerare aspetti degli scacchi – storico, simbolico ed estetico – che sono forse considerati con minor attenzione rispetto all’agonismo dei tornei nazionali o internazionali, ma che destano tuttavia interesse e piacere all’appassionato del gioco. Pertanto, mentre la parte centrale dell’articolo è dedicata alla bellezza negli scacchi e nella matematica, essa verrà anche considerata in altri ambiti, come nel gioco del Go, nell’arte, nella natura e nella scienza. Scopriamo così che esistono diversi criteri di valutazione della bellezza e che tra le sue principali caratteristiche troviamo le giuste proporzioni, l’armonia, le simmetrie e la capacità di stupire ed emozionare.
La bellezza
La bellezza ha sempre affascinato l’uomo. Gli antichi greci provavano stupore per la bellezza e filosofavano sotto la suggestione della meraviglia di fronte alla perfezione del mondo che chiamavano “cosmo”: il mondo ordinato dal“caos”, cioè dal vuoto smisurato. Cominciando da Pitagora, il cosmo è concepito come un universo ordinato e perfetta armonia, come una sostanza vivente, eterna e divina. Attraverso la conoscenza del cosmo – diceva Pitagora – l’uomo si avvicina alla sua natura originaria, e in questo contesto egli prescriveva lo studio della matematica. Inumeri, in particolare, hanno un significato mistico e sono la chiave per penetrare il mistero dell’universo divino e coglierne la struttura armonica. Questa concezione del mondo come cosmo è un messaggio tra i più belli che la sapienza greca abbia saputo trasmettere al pensiero occidentale. Per Platone valeva l’ideale della “bellezza-bontà”: tutto ciò che è bello è anche vero e buono e viceversa. Pertanto, la bellezza delle Idee che attira l’amore intellettuale del filosofo è anche il bene dell’uomo. Il fine della vita umana diventa così la visione delle Idee eterne e la contemplazione del Bene. Aristotele osservava che la bellezza dipendeva dalle proporzioni e dalle simmetrie e riteneva che la matematica potesse esprimere il senso della bellezza. La geometria di Euclide era considerata bella,alludendo all’austera bellezza del ragionamento matematico. Bertrand Russell, parecchi secoli dopo, scriveva che la matematica possedeva non solo verità ma anche suprema bellezza. Paul Dirac2 ha dichiarato di essere sempre stato motivato nelle sue ricerche dal principio della “bellezza matematica”.
Anche giochi strategici, come gli Scacchi e il Go, hanno una loro bellezza ed armonia e sono tenuti in alta considerazione per il piacere intellettuale che offrono all’animo umano. Basti pensare che nel Medioevo la bravura nel gioco degli scacchi era una delle virtù più importanti da coltivare per poter essere considerato un bravo cavaliere e che, nell’ordine monastico dei Domenicani, gli scacchi venivano addirittura utilizzati come fonte di ammaestramento morale.
La bellezza negli scacchi

Ricordando che il gioco degli scacchi è nato in India tra il V e il VI secolo, ed è arrivato in Europa solo agli inizi del Medioevo, grazie alla mediazione di Arabi e Persiani, sembra naturale cercare di comprendere il particolare significato che l’antica India offre del simbolismo negli scacchi. Gli scacchi e la scacchiera vengono interpretati attraverso il simbolo del mandala, che nasce come mezzo di ricerca della conoscenza in ambito spirituale. Il mandala rappresenta, secondo gli induisti e i buddhisti, il processo mediante il quale il cosmo si è formato dal suo centro e, attraverso un articolato simbolismo, consente una sorta di viaggio iniziatico che permette di crescere interiormente. Mandala significa centro, circonferenza, cerchio magico ed è rappresentato da un diagramma costituito nella sua essenza da un cerchio oppure da un quadrato. Nella maggior parte dei casi è proprio l’associazione di queste due figure geometriche, precisamente il cerchio inserito e protetto da un quadrato, con l’aggiunta di infiniti altri elementi, che realizza il mandala.

Negli scacchi il supporto sul quale si svolge il gioco, è una specie di mandala a 64 quadrati, che presenta grandezza e caratteristiche identiche a quelle di una particolare categoria di mandala, cioè il tracciato che veniva utilizzato come pianta in fase di edificazione di templi e città. Si desume da ciò che il simbolismo nascosto negli scacchi non è solo da ricercarsi nel gioco vero e proprio, ma anche nella scacchiera ed è in effetti su questa che la contrapposizione tra i due diversi schieramenti ha luogo. La scacchiera diventa così la rappresentazione della manifestazione del mondo, che nelle intenzioni di Shiva, il dio indù distruttore-trasformatore dell’universo, si deve organizzare secondo un ritmo quaternario. La scacchiera si può quindi vedere come costituita da quattro sotto quadrati disposti intorno ad un ipotetico e invisibile punto centrale: il bindu. In accordo con la cosmologia induista, ne consegue che la vita dell’intero universo, dal momento della sua nascita a quello della sua dissoluzione, si sviluppa in quattro ere (yuga).Altrettanti sono gli stadi che caratterizzano, sempre secondo gli indiani, la vita di un essere umano, così come quattro sono le stagioni e le fasi di una giornata.
I pezzi sulla scacchiera, nella loro posizione originale, ricostruiscono il modello strategico militare più in voga nell’antico oriente. Le forze armate leggere (i Pedoni) costituiscono le prime file e hanno lo scopo di proteggere e salvaguardare le truppe pesanti composte dai carri da guerra (le Torri), dai cavalieri (i Cavalli) e dagli elefanti da combattimento (gli Alfieri), mentre il Re e la Regina si tengono al centro delle truppe. In questa ambientazione ha luogo la battaglia che simbolicamente contrappone le forze della luce a quelle delle tenebre: i Deva (gli dei) contraddistinti dal colore bianco, contro gli Asura (i demoni), caratterizzati dal colore nero. E’ come se bene e male non esistessero di per sé, ma fossero solo il frutto della lotta che contrappone queste entità. Come se Deva e Asura acquistassero una fisionomia distinta, e un ruolo antagonista, solo perché impegnati sul terreno di battaglia, perché chiamati a interpretare Lila, il gioco di Dio. E’ questo forse il messaggio simbolico più importante che il gioco degli scacchi vuole trasmettere e, in tal senso, il parallelismo con il poema epico della Bhagavadgita3 (Il canto del Beato) è altrettanto evidente: Arjuna, protagonista della Gita (Canto), così come il giocatore di scacchi, è incitato daKrishna, una delle divinità induiste più popolari e venerate, a combattere la giusta battaglia dell’esistenza umana.
In relazione al simbolismo indiano, vediamo qui sotto una scacchiera come mandala meditativo.

La versione indiana degli scacchi

Il nome sanscrito “chaturanga”, che letteralmente significa “i quattro angoli”, si riferiva alla “quadruplice armata” ed alla divisione dell’esercito in fanti, cavalli, elefanti e carri, di cui rimane traccia nella suddivisione dei pezzi in pedoni, cavalli, alfieri e torri. Dall’India il gioco è passato in Persia col nome di chatrang, e la conquista araba del secolo VII lo ha introdotto fra i musulmani col nome di chatranj: a questi si deve l’introduzione del Visir, che doveva stare vicino al Re. Le regole del gioco erano leggermente diverse da quelle di oggi: il Re, la Torre e il Cavallo si muovevano come negli scacchi moderni, ma i Pedoni non potevano essere spinti di due passi alla prima mossa, l’Alfiere si muoveva in diagonale di due sole caselle e poteva “saltare” sopra i pezzi (come fa il Cavallo) e la Regina si muoveva solo in diagonale di una casa alla volta. Il Matto e lo Stallo erano gli stessi di oggi.
Perfino i Califfi giocavano a scacchi ed erano estremamente generosi con i loro campioni, riempiendoli d’oro e di doni. Naturalmente battere a scacchi un Califfo poteva essere pericoloso e costare anche la vita. Tuttavia i Califfi erano di solito spettatori e si divertivano a seguire le partite dei loro campioni preferiti, ma se il loro campione perdeva poteva anche cadere in disgrazia e perdere tutti i suoi privilegi di corte. Non solo i Califfi e i loro figli giocavano a scacchi, ma anche le principesse arabe. Molte poesie recitano di come i giocatori fossero distratti dalle grazie delle loro avversarie fino a perdere le partite, e gli scacchi potevano trasformarsi in un’occasione d’incontri galanti. Il contributo degli Arabi allo sviluppo ed approfondimento del gioco fu notevole, grazie soprattutto ad alcuni sovrani mussulmani appassionati del gioco. E’ noto il caso del Califfo Haroun-al-Rachid che aveva offerto un gioco degli scacchi a Carlomagno. Compaiono anche i primi libri di scacchi. Nell’anno 842 Al-Adli scrive il “Libro degli Scacchi”, dove presenta una raccolta di finali con intenti didattici. Nell’anno 847, Haroun-al-Rachid organizza il primo “match” della storia degli scacchi, in cui vince il persiano Ar-Razi che ha la meglio su Al-Adli. Il più forte giocatore dell’epoca era però Al-Suli, vincitore di Al-Maouardi, il campione di Haroun-al-Rachid tra il 900 e il 920, che mantiene la sua superiorità per quasi tutto il X secolo. Alcuni suoi finali di partita, particolarmente belli e sorprendenti, sono stati menzionati nei manoscritti di Al-Adli e di Al-Suli e sono stati pubblicati [2, 3].
Un problema di Al-Suli ci è stato tramandato con un piacevole aneddoto. Un giovane Signore, follemente appassionato del gioco degli scacchi, aveva commesso l’imprudenza di scommettere la sua schiava favorita Dilaram in cambio di un pegno in oro dell’avversario. Ridotto in una posizione inferiore e in presenza di una minaccia di matto in una mossa, non sa più cosa fare, si dispera e maledice la sua cupidigia che lo espone a perdere la donna che adora. Ma la bella Dilaram che, dietro al suo velo, aveva seguito la partita con grande attenzione, non desiderando diventare proprietà di uno straniero, così sussurra al suo padrone:” Oh! mio Signore, che la gioia entri nella vostra anima. Sacrificate le due Torri, piuttosto che sacrificare me, avanzate con audacia il vostro Elefante (Alfiere), spingete il vostro Pedone ed il vostro Cavaliere (Cavallo) darà matto!” Anche se un pò incredulo, il giovane Signore segue il consiglio della sua favorita, vince l’oro e tiene con sé Dilaram.

1. Th8+ Rxh8 2. Af5+ Th2 3. Txh2+ Rg8 4. Th8+ Rxh8 5. g7+ Rg8 6. Ch6#. Brava Dilaram !
Durante il Medioevo il gioco si era diffuso in tutte le corti e nei più famosi castelli, divenendo in breve tempo da gioco dei Re il re dei giochi. Nei secoli successivi gli scacchi sono stati praticati da Persiani e Arabi, che lo hanno introdotto in Europa verso il secolo IX o X, grazie alle crociate e ai Mori di Spagna. L’innovazione europea era stata quella di sostituire il Visir con la Regina, ma solo verso il secolo XV, al tempo di Isabella di Spagna, Lucrezia Borgia e Caterina Sforza, la Regina aveva ottenuto la sua completa libertà di movimento e acquistato il suo ruolo fondamentale. Infine, nel XVII secolo, il gioco si era assestato nella forma che conosciamo oggi.
Il gioco degli scacchi, nato come rappresentazione di una battaglia tra due eserciti, è stato spesso usato come metafora dei vari aspetti della vita. Intanto notiamo come nella trasposizione tra le diverse culture cambino le raffigurazioni e i nomi dei pezzi. L’elemento più variabile tra i pezzi è sicuramente l’Alfiere, che negli scacchi indiani è l’Elefante, nei paesi di lingua inglese il Vescovo (Bishop) e in quelli di lingua francese il Giullare (Fou). Queste diverse rappresentazioni derivano probabilmente dai diversi aspetti della vita di corte nelle diverse culture. Dopo tutto i pezzi degli scacchi moderni sono anche una rappresentazione della corte medievale. Infine ricordiamo come gli scacchi si siano prestati a varie interpretazioni, secondo i punti di vista psicologico, sociologico e storico, e spesso siano stati raffigurati nella pittura e descritti nella letteratura [4].
La bellezza nel Go
Il gioco del Go è uno dei giochi più diffusi nel mondo in termini di teoria ed attività intellettuale, alla pari degli Scacchi, nelle sue varianti Occidentali e Asiatiche (Shogi). È noto come wéiqí in Cina, igo o go in Giappone, e badukin Corea. Il go ha avuto origine in Cina, dove è giocato da almeno 2500 anni, è molto popolare in Asia orientale e più recentemente si è anche diffuso nel resto del mondo, ma non come meriterebbe, se si considera la natura del gioco e la sua bellezza intrinseca. Nel secolo VIII il gioco aveva raggiunto il Giappone, dove era molto popolare alla corte imperiale e, all’inizio del secolo XIII, si era diffuso anche tra il popolo. Nel 1603 Tokugawa Ieyasu aveva creato un governo nazionale unificato in Giappone e nominato Ministro del Go il miglior giocatore di go giapponese, il monacobuddhista Nikkai (Kano Yosaburo), che aveva assunto il nome di Honinbo Sansa e fondato la scuola di Go Honinbo.Altre scuole fondate successivamente incrementarono enormemente il livello del gioco e introdussero il sistema di classificazione in dan e kyu dei giocatori. A parte la dimensione della tavola, le regole sono state mantenute nei secoli, cosicché si può considerare il go il gioco più antico in assoluto. In molte culture dell’Estremo Oriente era considerato una delle arti in cui una persona di alto livello culturale doveva essere versata. In Cina era il gioco dell’aristocrazia ed una della quattro arti dello junzi (il gentiluomo cinese), assieme alla calligrafia, alla pittura e alla musica.
Il pannello di Kanō Eitoku mostra alcuni cinesi dell’epoca della dinastia Ming che giocano a Go (XVI secolo).

E’ probabilmente il gioco più complesso che esista, dato il vasto numero di varianti che si incontrano nelle partite, e per le difficoltà che si incontrano nella programmazione su computer. Mentre il più forte software scacchistico –Deep Blue – ha battuto il campione del mondo Garry Kasparov nel 1997, i programmi commerciali di go si trovano spesso nel range amatoriale 1-10 kyu e possono facilmente perdere con adolescenti di talento. I ricercatori nel campo dell’Intelligenza Artificiale ritengono che il go richieda la programmazione di molti più elementi per poter simulare il pensiero umano che non gli scacchi e che rappresenti un test critico per misurare la capacità di un computer. Tuttavia, recenti progressi nel campo dell’Informatica hanno permesso ad alcuni software di go di raggiungere il livello amatoriale di alcuni dan, e, su scacchiere 9×9, alcuni di questi software sono oggi in grado di competere con giocatori professionisti.
Il Go è anche considerato un modello di ispirazione per la ricerca in Matematica, a seguito delle sue regole semplici ed eleganti. La bellezza di questo gioco sta proprio nella semplicità delle regole, a cui corrisponde una grande difficoltà nello svolgimento, e soprattutto nel coinvolgimento totale in cui si immerge il giocatore. Anche il Go ha un simbolismo intrinseco non differentemente dagli scacchi. Il Go-ban (go è il nome del gioco e ban significa letteralmente “sequenza” o “successione”) ha 360 punti (intersezioni), uno per ogni giorno dell’anno; il susseguirsi di mosse e contromosse ricorda l’eterno alternarsi d Yang (Bianco) e Yin (Nero), e l’insinuarsi di territori bianchi nel campo nero e viceversa, altro non è che il ridisegnare, di volta in volta in forme sempre nuove, il noto simbolo del Tao, la Via.

Tao significa letteralmente la Via o il Sentiero. Spesso tradotto come il Principio, è uno dei principali concetti dellafilosofia cinese. È l’eterna, essenziale e fondamentale forza che scorre attraverso tutta la materia dell’Universo, vivente o meno. Il Tao è solitamente associato al Taoismo, ma anche il Confucianesimo fa riferimento a esso.
I giocatori collocano alternativamente pedine (pietre) nere e bianche sulle intersezioni vuote di una scacchiera dotata di una griglia 19 × 19. Lo scopo del gioco è il controllo di una parte di territorio maggiore di quella dell’avversario. I giocatori cercano di disporre le proprie pietre in modo che non possano essere catturate, ritagliandosi allo stesso tempo dei territori che l’avversario non possa invadere senza essere catturato. È infatti possibile catturare una pietra o un gruppo di pietre avversarie circondandole completamente con le proprie pietre, in modo che non abbiano intersezioni libere (libertà) adiacenti. Disporre le pietre vicine tra loro permette di rafforzarle a vicenda ed evitarne la cattura e, d’altro canto, disporle distanti tra loro permette di creare maggiore influenza su tutto il goban. Parte della difficoltà strategica del gioco consiste proprio nel trovare un equilibrio tra queste opposte necessità: i giocatori cercano di soddisfare contemporaneamente le esigenze offensive e difensive e scelgono tra priorità tattiche e piani strategici. Il gioco termina quando i giocatori passano consecutivamente, indicando che non sono più in grado di incrementare il proprio territorio o diminuire quello dell’avversario. Durante l’elaborazione della strategia ogni giocatore cerca di “leggere nella mente” dell’avversario ed intuire, a partire dal suo comportamento osservabile, quali siano le sue rappresentazioni mentali e le sue intenzioni.
E’ noto che il campione di scacchi Emanuel Lasker era solito, nei giorni precedenti un incontro di scacchi o un match, giocare a Bridge oppure a Go, gioco di cui ammirava la semplicità, l’eleganza e la logica delle regole. Il suo libro “Popular Board Games” (Berlino 1931), che descrive alcuni dei più popolari giochi da tavolo, tra cui scacchi, go, dama e backgammon, dedica un’importante parte alla descrizione dell’antico gioco nazionale giapponese. Lasker riteneva che il gioco del Go superasse il gioco degli Scacchi nella semplicità delle regole, ma che lo eguagliasse nella sua ricchezza di fantasia e bellezza. In un’intervista in cui gli era stato chiesto se avesse giocato a Go da molto tempo, Lasker rispose nel suo consueto stile: ”Ho cercato di penetrare i segreti di questo gioco da circa 50 anni. Ho più o meno decifrato la tattica, ma non la strategia. Apparentemente, questo mi prenderà altri 50 anni”[5].
Leggendari giocatori di Go sono stati Honinbo Dosaku (1645-1702), Honinbo Shusaku (1829-1862) e Go Seigen (Wu Qingyuan), nato nel 1914. Nel secolo scorso, il grande giocatore di go Honinbo Shusai Meijn, che rappresentava la più alta autorità e tradizione del Go in Giappone, è stato protagonista di importanti match, tra cui quello nel 1933 con Go Seigen e nel 1938 con Kitani Minotu. Per i suoi incredibili successi, Go Seigen è stato considerato da molti il più grande giocatore del XX secolo e di ogni tempo. Assieme a Kitani Minoru ha sviluppato e diffuso un particolare schema di apertura (Shinfuseki), in contrapposizione agli schemi d’apertura tradizionali, e per questo importante contributo, Go Seigen e Kitani Minotu sono considerati i padri del Go moderno. Una bella descrizione dello spirito che anima questo gioco orientale è presentato nel libro del Premio Nobel per la letteratura Kawabata Yasunari “Il Maestro di Go” [6], che racconta la transizione del Giappone all’età moderna attraverso una sfida di go, che si è realmente svolta nel 1938, tra il vecchio maestro Shusai e il giovane sfidante Otaké (Kitani Minoru), bandiera della “nouvelle vague” del gioco.
Go e Scacchi
Il paragone tra questi due giochi strategici sembra a questo punto inevitabile, anche se non è immediato. I due giochi sono molto diversi, anche se vi sono alcuni “legami di parentela”. Le differenze più evidenti riguardano lo spazio, ilmateriale, e il fine del gioco. Lo spazio degli scacchi è piccolo e vi è una notevole circolazione di pezzi, mentre lo spazio nel go è immenso, ma si popola e si restringe fino alla saturazione. Il materiale è completamente presente all’inizio di una partita a scacchi, i pezzi sono molto diversi e si muovono in modo ben definito, mentre le pietre del go, bianche e nere, sono tutte uguali e hanno lo stesso valore, anche se questo è costantemente variabile durante la partita. Lo scopo negli scacchi è la distruzione del Re avversario, lo scacco matto, mentre nel go lo scopo è quello di conquistare territorio, e fare meglio dell’avversario. Nel go un vantaggio anche minimo (0.5 punti) è sufficiente a garantire la vittoria ed è persino possibile sopprimere per convenzione la patta. Nel go lo spazio e la sua occupazionecostituiscono lo scopo del gioco, e la parziale distruzione dell’avversario è un mezzo, mentre negli scacchi è il fine. Da qualunque prospettiva lo si guardi, sia essa di spazio, di tempo, di tattica o strategia, di fasi del gioco, di studio, di mosse forzate, d’iniziativa, ecc., i parametri sono diversi, ma c’è un legame, più o meno evidente, che assimila le azioni di un giocatore di scacchi a quelle di un giocatore di go.
La bellezza negli scacchi e nella matematica
Lo svolgersi di una partita di scacchi nelle varie fasi del gioco ha qualcosa in comune con l’esperienza dello studio matematico. Il piacere in matematica, come negli scacchi, è in stretta relazione con la conoscenza che si ha di essi. Il piacere nella matematica, che si prova quando si capisce qualcosa di nuovo e che necessita di un precedente sforzo di volontà e intelligenza, la rende estremamente bella. I modelli del matematico, come quelli del “chess-player”, del pittore, del poeta, del musicista devono essere belli e i vari elementi devono combaciare in modo armonico. Quando alla fine si raggiunge il risultato, lo scenario che si presenta può essere paragonato al più bel quartetto da camera, alla natura più rigogliosa o al piacere più estatico. In conclusione, possiamo dire che le qualità di un bravo scacchista sono simili, anche se non proprio le stesse, a quelle che caratterizzano un buon matematico.
Kandinsky4

Per esempio, nella fase di apertura il giocatore utilizza le sue conoscenze di teoria per impostare un particolare piano di gioco, così come il matematico, affronta un problema usando quei particolari strumenti che gli servono nel caso specifico. L’impianto di sviluppo di un’apertura negli scacchi è, nei suoi vari aspetti, simile allo sviluppo di un problema in matematica. Nel centro-partita la creatività e l’intuizione si fondono con le capacità logiche necessarie per “vedere” una situazione in evoluzione, così come la scoperta matematica necessita di un coinvolgimento totale delle diverse capacità umane allo scopo di trovare un collegamento prima sconosciuto. II finale è la parte più tecnica della partita e l’unica completamente teorizzabile. Nei vari tipi di finale si può determinare il vincitore ed anche la procedura che porta alla vittoria, come avviene in matematica quando, scritte certe equazioni, si sa che il problema può essere portato alla soluzione utilizzando tecniche note.
Un ulteriore elemento comune alle due discipline è il rapporto tra concretezza e astrazione. La capacità di astrazione necessaria per poter far bene matematica deve essere opportunamente compenetrata nella fase didattica con l’esigenza di concretezza del neofita, così come nel gioco degli scacchi vanno attentamente calibrate l’esigenza di concretezza (spostare i pezzi sulla scacchiera) con la necessità di astrazione della regola “pezzo toccato, pezzo mosso”, che impone di saper “vedere” la posizione in evoluzione senza toccare i pezzi.
Esempi e modelli
Più ancora della partita, il problema di scacchi è simile ad un problema matematico. Alle considerazioni precedenti si aggiungono ora la fase di impostazione e la coincidenza degli obiettivi, cioè, in entrambi i casi, c’è un problema da risolvere. La formulazione del problema è univoca e rigorosa e occorre intraprendere il ragionamento studiando le proprietà del quesito.
Un giocatore con una buona conoscenza degli scacchi ha probabilmente letto il “Lasker’s Manual of Chess”[7]. Questo testo scritto da un campione di scacchi, oltre che matematico e filosofo, è imbevuto dello giusto spirito, per cui gli scacchi non sono considerati come un semplice gioco, ma piuttosto come un metodo di “mind training”. In se stesso il gioco non è di nessuna utilità, ma nella misura che è tipico della lotta (struggle), del desiderio di progresso, della stessa vita, l’autore lo considera parte dello schema generale delle cose. Il trattato è composto di sei Books in cui vengono presentate la Teoria delle Aperture, la Combinazione, il Gioco di Posizione, oltre ad alcuni Esempi e Modelli. Nel Book IV (Il Gioco di Posizione) viene anche esposto un concetto etico, quando Lasker descrive la relazione tra gli scacchi e la vita e scrive che “il gioco degli scacchi è uno dei santuari in cui il principio di giustiziadeve occasionalmente rifugiarsi per ritrovare sostegno e respiro di fronte all’armata di mediocrità che lo respinge dal mondo. E molti uomini colpiti dall’ingiustizia, come Socrate e Shakespeare, avendo trovato la giustizia realizzata sulla scacchiera, hanno ritrovato il coraggio e la vitalità per continuare a giocare il gioco della Vita”. Nel Book V viene presentato l’Effetto Estetico negli Scacchi, che si manifesta nel momento stesso in cui uno studioso o uno spettatore, seguendo gli avvenimenti sulla scacchiera con interesse e comprensione, prova un’intera scala di sentimenti dovuti al gioco dei pezzi e risponde al “charm” del conflitto scacchistico.
Molte posizioni antiche di secoli ci sono state tramandate per il loro aspetto estetico. Un aspetto affascinante si ha quando vediamo che la forza brutale non ottiene il successo e viene vinta dalla forza dello spirito. Quando la mente supera la materia siamo incantati. Negli scacchi la forza è composta dal numero, dalla forza, dalla mobilità dei pezzi e dalle difficoltà del compito richiesto. Se questa forza brutale è sopraffatta dal numero inferiore, dalla minor forza, da mosse che indicano più debolezza che forza, e che sembrano annunciare sconfitta più che trionfo, dal potere dello spirito, da un’idea che, apparentemente assurda, è in realtà la verità stessa, allora siamo deliziati. E’ la storia di Davide e del gigante Golia.
Vediamo alcuni esempi tratti dal Manuale di Lasker con i suoi commenti:

Il compito da attuare è difficile. Si deve vincere una forte opposizione e dare lo Scacco Matto in due mosse. Tuttavia, la soluzione del problema non comporta alcuna dimostrazione di forza, come dare scacco o catturare un pezzo nemico. Invece, il più forte pezzo del Bianco si offre in sacrificio con la mossa Th6, e tuttavia questa mossa – quasi assurda – risolve da sola il problema e mostra la verità.
L’ideale dei nostri progenitori è stata la partita giocata a Londra nel 1851 da Anderssen contro Kieseritzki, definita la “Partita Immortale”.
La Partita Immortale

1.Ad6 DxT+ 2. Re2 AxT 3. e5!! Ca6 4. Cxg7+ Rd8 5. Df6+ CxD 6. Ae7 Matto.
Tuttavia, l’apertura della partita “offende” la sensibilità moderna dei giocatori, ma i nostri progenitori non erano sufficientemente sensibili allo svolgimento della fase d’apertura. Questa partita è stata anche presentata e discussa in dettaglio nel libro di David Shenk “Il Gioco Immortale” [2].
La seguente posizione, tratta da un antico manoscritto persiano, mostra la brillante conclusione delle operazioni di due Cavalli che salvano il Bianco da una situazione disperata.
Da un antico documento persiano

La posizione del Bianco sembra molto compromessa. Ogni parte sta attaccando un Cavallo, ma il più importante è che il Nero minaccia Matto. Il Bianco non ha difesa, per cui può solo contrattaccare, ma i Cavalli del Nero si oppongono a questo piano, finché un’idea brillante del Bianco li obbliga a cooperare col nemico (!)
- Th7+ Rg8 2. Cf6+ Rf8 3. e7+ Cxe7 4. Tf7+ CxT 5. Ce6 Matto
Il matto è notevole per la sua economia. In verità, le Torri ed il Pedone del Nero non sembrano necessari, ma nei tempi antichi erano utili come coreografia di una strenua battaglia.
Infine uno studio di Rinck, apprezzabile per la bellezza, economia e precisione della composizione.
Henry Rinck

Il Pedone Passato in g6 può essere solo sostenuto dall’Alfiere bianco ed essere attaccato dalla Torre nera sulla colonna g, poiché l’azione della Torre sulla colonna f è ostacolata dal Pedone nero (ostruzione). Tuttavia, l’Alfiere è in grado di bloccare la colonna g facendo uso di vari motivi: con 1. Ae3 controlla la casa g1 e blocca la colonna g, per cui la Torre nera gioca: 1….Tf3. Dopo la mossa della Torre nera Il Bianco vince in ogni caso con 2. Ag5. Infatti, dopo 2…f6 x A, il Pedone ostruisce la colonna g, e se invece il Bianco gioca 2…Tg3 il Nero con 3. Ah4 inchioda la Torre. Il Pedone non può essere fermato.
Problemi e Combinazioni
A questo punto presentiamo alcuni problemi di scacchi, seguendo l’opinione di Godfrey Hardy5 : ”Un problema di scacchi è autentica matematica, ma è in certo senso matematica “banale”. Per quanto complicato e ingegnoso sia, per quanto originali e sorprendenti siano le sue mosse, gli manca qualcosa di essenziale. I problemi di scacchi non sono importanti. La migliore matematica non solo è bella, ma è anche seria. Non mi riferisco alle applicazioni pratiche della matematica. La “serietà” di un teorema matematico non dipende dalle sue applicazioni pratiche, che di solito sono irrilevanti, ma dalla significatività delle idee matematiche che esso mette in relazione. In termini approssimativi si può dire che un’idea matematica è “significativa”, se la si può collegare in modo naturale e illuminante a una vasta rete di altre idee matematiche. Perciò un teorema matematico serio, un teorema che colleghi idee significative, porterà molto probabilmente grandi progressi in matematica ed anche nelle altre scienze. Nessun problema di scacchi ha mai influenzato lo sviluppo generale del pensiero scientifico, mentre Pitagora, Newton, Einstein, ciascuno nella propria epoca, né hanno cambiato l’intero corso”[8]. Alcuni di questi teoremi sono semplici, sia nell’idea che nell’esecuzione, e ciascuno conserva la freschezza e l’importanza di quando è stato scoperto. Uno dei teoremi più celebri della matematica greca è dovuto a Euclide e consiste nella dimostrazione dell’esistenza di un numero infinito di numeri primi. E’ una dimostrazione per reductio ad absurdum, che è una delle più belle armi del matematico. I numeri primi sono quei numeri come 2, 3, 5, 7, 11, 13, 19, 23, 29…che non possono essere scomposti in prodotto di fattori minori, e costituiscono il materiale da cui, attraverso la moltiplicazione, si costruiscono tutti i numeri Per esempio 37 e 317 sono numeri primi, mentre il numero 666 non lo è: infatti è uguale al prodotto dei seguenti numeri primi 2x3x3x37. Ogni numero che non sia numero primo è divisibile per almeno un numero primo (in genere per molti) ed Euclide dimostra che esistono infiniti numeri primi, cioè che la successione non termina mai. La dimostrazione per reductio ad absurdum è un gambetto molto più raffinato di un gambetto di scacchi: un giocatore di scacchi può offrire in sacrificio un pedone o un pezzo, ma il matematico offre tutta la partita [8].
I primi problemi di scacchi ci sono stati trasmessi da manoscritti arabi intorno al IX secolo – il problema di Abu’n-Na’am è dell’anno 840 circa – mentre occorre attendere il XIII secolo per trovare problemi in manoscritti italiani, come il Bonus Socius del 1266 [3].
Bonus Socius, 1266

Soluzione: 1. Tc8+ Ra7 2. Tc7+ Ra8 3. Ta7+! Rxa7 4. Cc6+ Ra8 5. Tb8#. Notiamo che la presenza delle Torri nere in f2 e g3 è in realtà superflua, essendo state inserite solamente per preservare l’equilibrio materiale.
Va anche detto che, mentre le regole attuali del gioco degli scacchi sono state fissate verso la fine del XV secolo (manoscritto di Gottinga di Lucena), i primi problemi sono stati composti intorno al XVIII secolo. Oltre al siriano Philipp Stamma, i più noti compositori erano Ercole del Rio (Sopra il giuoco degli scacchi, 1750), Giambattista Lolli (1763) e Domenico Ponziani (Il giuoco incomparabile degli scacchi, 1769).
Dal libro “Sopra il giuoco degli scacchi”:
Ercole del Rio, 1750

Soluzione: 1. Tf8+! Rg7 2. Ah6+! Rxh6 (forzata) 3. Tg8!! – una mossa tranquilla, una novità a quell’epoca – 3…Af5 4. Txf5 5. Th5#. Qualunque sia la risposta del Nero segue 4. Th5+! Axh5 5. g5 Matto
Un problema del compositore Joseph Kling6, tratto dal manuale di Howard Staunton del 1847 [9].
J. Kling, 1847

Soluzione: 1. O-O h5 2. Rh2 h4 3. Ag1 h3 4. Tf2 Rd4 5. Tf4++ e Matto.
Un problema del compositore e diplomatico britannico Gerald Frank Anderson7
G. F. Anderson, 1921

La soluzione del problema di Anderson è particolarmente difficile e sorprendente. Elemento caratteristico è ilcontro-scacco, ovvero il rispondere a uno scacco con un altro scacco. Nel diagramma il Bianco ha a disposizione unoscacco di scoperta apparentemente letale. Muovendo l’Ab3 si dà scacco con la Tb1. La Tb1 è però attaccata dall’Alfiere nero in h7 e su 1. Aa4++ oppure 1. Ac2+ il Re nero ha a disposizione la casa c4 e il Bianco non ha il matto.
La sorprendente soluzione è 1. Rd6! che minaccia 2. Db7#, ma che si espone allo scacco della Torre nera. Dopo 1. …Td3+ la Torre in d3 interferisce con la linea d’azione dell’Alfiere in h7 e permette il matto: 2. Ad5# oppure, in modo simile, dopo 1. …Tg6+, segue 2. Ae6 Matto.
Un problema di Samuel Loyd8, il padre della scuola americana.
S. Loyd, 1859

Soluzione: 1. Taf2! a4 (forzata) 2. Rd2!! a3 3. Ta1! a2 4. Re1!! Grazie a questa mossa, l’Alfiere nero può giocare e prendere la Tf2 con scacco, ma con 5. Rxf2 il Bianco da matto.
Tutte le mosse del Bianco sono giocate sottilmente, una dopo l’altra, su case scelte in modo molto preciso, come in un ingranaggio perfettamente funzionante.
Viene in mente quanto scrive Capablanca in “Chess Fundamentals”[10] a proposito della coordinazione dei pezzi nel medio-gioco e nelle varie combinazioni sulla scacchiera: “Appena si presenta l’occasione tutti i pezzi entrano in azione ‘en masse’, se necessario, e coordinano la loro azione con machine-like precision”.
Per concludere questa parte sulla bellezza negli scacchi vediamo alcune posizioni di centro-partita illustrate nei libri di Capablanca: “Chess Fundamentals” [10] e “My Chess Career”[11].
Scrive Capablanca: “Consideriamo alcune combinazioni che spesso scaturiscono durante una partita e possono dare un’idea della bellezza del gioco, una volta che il giocatore ne abbia acquisito la necessaria conoscenza”[10]
1. Questa posizione si è verificata durante una partita giocata al Manhattan Chess Club di New York nell’anno 1906.
Attacco senza l’aiuto dei Cavalli

Dopo la mossa 29. Tc1! Il Nero gioca 29…Dxf2? e dà l’opportunità al Bianco di terminare in modo brillante. La mossa 29…Dxf2 permette al Bianco di portare l’altra Torre nella rete di matto 30. Tf1! Dd4 31. Tf5 e6 e segue matto in tre mosse dopo 32. Txa7+! (32…DxT 33. Ta5 Tb7 34. DxT Matto). Tuttavia, sembra che con 29…Dd4 Raubitschek avrebbe potuto ottenere la patta.
Così commenta Capablanca: “L’ultima mossa del Nero 31…e6, è stata giocata per bloccare quella che il Nero pensava essere la minaccia del Bianco, i. e. 32. Ta5 , a cui avrebbe risposto con Df4+ e ottenuto la patta per scacco perpetuo. Il Bianco, tuttavia, aveva in serbo una mossa più forte, ed ha potuto dare matto in tre mosse come segue: 32. Txa7+ DxT 33. Ta5 il Nero muove e il Bianco da Matto.”
1. Un’altra posizione ottenuta al Manhattan Chess Club contro Raubitschek:
Attacco senza l’aiuto dei Cavalli

”La mossa tocca al Nero, che ha un Cavallo ed un Pedone in meno, per cui deve vincere rapidamente, ammesso che ciò sia possibile. Il Nero gioca: 23…Td8-g8 24. Tf1-f2 (Se 24. DxD Txf2+ 25. Rh1 Ad5! e il Matto segue in poche mosse) Tg4xg2+ 25. Rg1-f1 Ae6-c4+ 26. Ca3xc4 Tg2-g1 Matto”
1. Questa posizione, che si è verificata nella partita d’esordio al Torneo di San Sebastiano nel 1911, illustra invece un esempio in cui l’attacco viene attuato con i Cavalli come forza prominente.
San Sebastian, 1911

Il Bianco ha due Pedoni in meno e deve quindi attaccare prontamente. La partita è continuata così:
1. Cf5xg7 Cc5. Un errore che facilita la vittoria, poiché il Bianco prende semplicemente la Torre col Cavallo e prosegue l’attacco.
Il Nero avrebbe dovuto giocare: 1…CxC, a cui sarebbe seguito 2. Cf6+ Rg6 3. CxA f6 (best) 4. e5 Rf7 5. Cxf6 Te7 6. Ce4 e la posizione del Nero non si tiene più. (Capablanca)
In My Chess Career [11], dove c’é il “full score” della partita, possiamo vedere la conclusione della partita: 28. Cfxg7Cc5 29. Cxe8 Axe8 30. D3e-c3 f7-f6 31. Ch5xf6+ Rg6 32. Cf6-h5 Th8-g8 33. F4-f5+ Rg6-g5
Il Nero avrebbe dovuto abbandonare invece di proseguire questa partita (Capablanca)
34. Dc3-e3+ Rh4 35 Dg3+ Rg5 36. h4 Matto.
“My Chess Career”, uno dei libri di scacchi più interessanti che abbia mai letto, assieme a “My System” di Nimzowitsch, “Masters of the Chess Board” di Reti e “The Middle Game in Chess” di Znosko-Borovsky, riporta una partita giocata contro Dus-Chotimirski a San Pietroburgo nel 1913, in cui la vittoria è ottenuta con un attacco indiretto. Dice Capablanca : “Spesso l’attacco nel medio-gioco viene condotto contro una Posizione o contro Pezzi opersino contro Pedoni”, dato che “Il guadagno di un Pedone tra giocatori di pari forza spesso significa la vittoria della partita [10].
L’interesse della partita, una delle più belle giocate da Capablanca durante la sua seconda visita in Europa, non consiste solo nella superlativa capacità tattica mostrata dal genio cubano, in grado di evolvere un improvviso attacco con la sua 25a mossa e nei commenti alla partita, ma anche nelle considerazione generali – che riporto sotto – che danno un’idea dell’evoluzione del suo stile di gioco nel periodo compreso tra i grandi Tornei di San Sebastiano (1911) e di San Pietroburgo (1914) e il Campionato del mondo con Lasker nel 1921. Scrive Capablanca ”I piani sono costruiti su ampie e solide linee, la visione è ampia e in molti casi le combinazioni, siano lunghe o corte, come pure le differenti manovre, sono solo mezzi tattici di evolvere differenti piani strategici. La concezione generale del gioco, la più alta qualità di un maestro di scacchi, è illustrata nei vari esempi, dove si vede che i piani sono svolti con accuratezza” [11].
La concezione generale del gioco di Capablanca è illustrata nelle varie posizioni riprodotte nei successivi tre diagrammi.
1. Posizione alla 25a mossa del Bianco:
St. Petersburg December 1913

“Durante la partita erano presenti, oltre ad alcuni maestri nazionali, due dei più forti giocatori del mondo, che pensavano che avessi permesso al mio avversario di ottenere una posizione vincente. Non avevano visto la mia venticinquesima mossa che doveva ribaltare il corso della battaglia”.
25. e5! g6. Per parare la minaccia del Bianco Df5.
26. e6 Tf8 27. Cg3! Db7. A 26…fxe6 seguiva Dg4, minacciando sia Bxg6 che Dxe6+. Adesso il Cavallo bianco entra in tutte le varianti con grande forza.
28. Cg5!

28…fxe6. 28…Rh8 era meglio, ma in questo caso De4 dovrebbe vincere. Il Nero voleva prendere questo Pedone da tempo, e pensa che sia giunto il momento, ma così facendo accelera solo il risultato.
29. dxe6 Dc7 30. Dc6!

Lo scopo di questa mossa è quella di controllare la casa e8 con la Regina e l’Alfiere, cosicché dopo il cambio delle Donne in d7, rimane l’Alfiere per proteggere l’avanzata del Pedone passato.
30…Dd8 31. CxA+ DxC 32. Axb5 Cc3 33. Dd7 DxD 34. BxD Tb8 35. e7 e il Nero ha abbandonato dopo alcune mosse”.
Fin qui Capablanca, ma noi vediamo il seguito della partita: 35. e7 Rf7 36. Te1 Te8 37. AxT+ RxA 38. Te6 d5 39. Rf1 Cb5 40. Re2 Cc7 41. Te5 Ca6 42. b5 Cc5 43. b6 d3+ 44. Rd2 Rd7 45. e8D+ Rd6 46. De7+ Rc6 47. Dxc5+ (1-0)
La continuazione della partita richiede piuttosto psicoanalisi che analisi scacchistica (Fred Reinfeld).
Il cubismo negli scacchi
Anche il gioco degli scacchi è rappresentato dal Cubismo9. Nel lavoro d’arte cubista gli oggetti sono frantumati, analizzati e riassemblati in forma astratta. L’artista, invece di dipingere i vari oggetti osservati da un solo punto di vista, dipinge i suoi soggetti visti da una moltitudine di punti di vista.
Juan Gris “Chess Pieces”, 1917

Nel 1923 Reti pubblica “Modern Ideas in Chess” in cui indica la strada che gli scacchi hanno percorso dal classicismo di Anderssen attraverso il naturalismo della scuola di Steinitz fino alle idee individuali dei maestri più moderni [12]. In questo testo innovativo, considerato il manifesto del movimento scacchistico “ipermoderno”, possiamo leggere come Tartakower descrive la nuova scuola: ”Anche gli Scacchi possono mostrare il loro “cubismo”. I suoi principali rappresentanti, Alekhine, Bogoliubow, Breyer e Reti, hanno ottenuto, specialmente negli anni 1920, splendidi successi contro i “big men” della scuola classica, come Rubinstein, Tarrasch, Maroczy, ed hanno di conseguenza attirato l’attenzione del mondo scacchistico sulla moderna scuola di scacchi. Tuttavia, i nuovi principi mostrano un certo grado di secessione rispetto ai principi classici, poiché mostrano piani che non si erano mai visti prima: schemi che danno al gioco un aspetto peculiare, mosse che sembrano beffare i principi del libero sviluppo dei pezzi, ed infine metodi che cercano la salvezza nel continuo accumulo di energia latente. Gli idoli della vecchia scuola sono infranti per effetto del pronunciamento rivoluzionario di Breyer: ”1. e4 è l’inizio del disgregamento del campo bianco”. Reti attenuerà questa asserzione dicendo che “il Bianco dopo aver aperto il gioco con 1. e4 si crea una situazione compromessa”. Gli innovatori Reti e Nimzowitsch sostenevano che era necessario diffidare sempre delle mosse naturali, come lo sviluppo di un pezzo o l’occupazione di una colonna aperta, poiché può sempre sussistere la possibilità di un “piano” più promettente. Paradossalmente, Reti affermava che allo scacchista le regole non devono importare più delle eccezioni [13].
Il maestro internazionale Nicolas Giffard, campione di Francia 1978 e 1982, nella sua Guida degli Scacchi [3] presenta i giocatori della “Scuola Ipermoderna” – in particolare Gyula Breyer (1893-1921) e Richard Reti (1889-1929) – come i “Nuovi Filosofi”, che hanno esplorato regioni del pensiero, di cui i teorici della scuola classica (Steinitz e Tarrasch) non avevano neppure sospettato l’esistenza.
Il vecchio principio di “Occupare il Centro della scacchiera con i propri Pedoni” era così naturale che nessuno avrebbe mai pensato di metterlo in dubbio.
Invece adesso ci si chiede:
“Perché si spinge un pedone (1. e2-e4 oppure 1. d2-d4) alla prima mossa?“
-Per abitudine.
-Ma come possono uscire i pezzi, se non si spinge un pedone centrale?
-Ci sono altri metodi.
-Ma in questo modo l’avversario con i suoi pedoni in centro potrà controllare il centro.
– No, l’occuperà solamente”.
Tutta la novità della concezione ipermoderna si fonda su questa sfumatura: “Un pedone non controlla la casa sulla quale si trova”, così come un pezzo d’artiglieria non può niente contro un nemico troppo ravvicinato. Breyer e Retinon negavano l’importanza del Centro, proponevano solo un nuovo metodo per assicurarne il dominio. In sintesi, la loro proposta era la seguente: “Lasciate i pedoni centrali nelle loro case iniziali, dove conservano tutto il loro potenziale per una spinta al momento propizio, sviluppate gli Alfieri in fianchetto (sulla grande diagonale), e con l’aiuto dei Cavalli e dei pedoni laterali (pedoni “c” e “f”) attaccate il centro dei pedoni nemici”.
Breyer considerava inoltre la spinta iniziale del pedone di Re (1. e2-e4) cattiva perché il Bianco offriva con la mossa di questo importante pedone centrale un obiettivo d’attacco al Nero. Al contrario, giudicava la spinta del pedone di Donna (1. d2-d4) del tutto corretta, poiché, malgrado l’allontanamento dalla sua base, il pedone “d” era protetto dalla Regina.
Il campione del mondo Alekhine, nel suo libro ”Gli Scacchi Ipermoderni”, riconsidera le precedenti dichiarazioni, ricordando che in realtà è possibile accettare l’impianto di ogni tipo di lotta, aperto o chiuso, combinativo o posizionale. In realtà, afferma, “ciò che conta non è la linea scelta, ma il senso generale della lotta” (Lasker). Riporta, come esempio delle nuove concezioni, una partita di Keres [14], in cui un Cavallo viene mosso in apertura sette volte nello spazio di tredici mosse, contravvenendo alla legge di rapido sviluppo10 e si domanda cosa avrebbero detto, di fronte ad un caso come questo, i seguaci della scuola dello sviluppo (Morphy) o i maestri posizionali (Steinitz-Tarrasch).
La caratteristica essenziale dell’Ipermodernismo – conclude Alekhine – consiste nell’intuizione che, al di sopra della strategia (posizioni, combinazioni), degli enunciati (sviluppo, evoluzioni), delle tattiche (lotte aperte, lotte chiuse), c’è l’idea, e che per servirla bisogna lanciarsi in una condotta tecnica e psicologica permeata da uno spirito di attivitàe precisione allo stesso tempo, e ribadisce che “la spina dorsale del moderno concetto di lotta scacchistica è semplicemente il piano” [13].
La bellezza nella matematica e nell’arte
La matematica possiede verità e bellezza, una bellezza senza appello, che trascende la nostra natura.
Kandinsky
Godfrey Hardy ha scritto in “Apologia di un Matematico”[8]: «Ogni paese civile conta innumerevoli giocatori di scacchi (in Russia quasi tutta la popolazione sa giocare a scacchi), che sanno apprezzare la bellezza del gioco o di un problema di scacchi. Un problema di scacchi non è altro che un esercizio di matematica pura (una partita non lo è del tutto, perché in essa entrano in gioco fattori psicologici). Ora, se un problema è definito ‘bello’ è la sua bellezza matematica che viene elogiata, anche se è una bellezza di un genere un pò inferiore. I problemi di scacchi cantano le lodi della matematica. Ed è la matematica “inutile”, la matematica pura, quella fine a se stessa, la matematica bella. Un altro elemento comune alle due discipline è l’estetica. La passione e il piacere del matematico che scopre e dimostra un teorema sono in qualche modo simili ai sentimenti dello scacchista che vince una partita o risolve un problema, per il compiacimento della forza delle idee sviluppate ed anche per il senso di armonia e di ordinata bellezza che produce il risultato.
Inoltre Andrew Wiles11 ha scritto che la matematica non è esclusiva della nostra civiltà, non è come un’opera d’arte o una sinfonia. La matematica, e in particolare la teoria dei numeri, che è la sua forma più pura, è qualcosa di comune in ogni angolo del sistema solare o dell’universo. La matematica fa parte della ragione stessa: per questo ha un’intrinseca bellezza, diversa da quella fugace delle opere d’arte, tanto più preziosa per la sua caducità. La matematica possiede quel genere di bellezza permanente, quasi fredda, che è eterna, perché fa parte della struttura stessa della ragione e della natura [15].
La geometria di Euclide è considerata bella per la bellezza che molte persone trovano nel ragionamento matematico. Anche formule matematiche possono essere considerate belle ed eleganti come, per esempio, la formula di Eulero(qui sotto riportata)
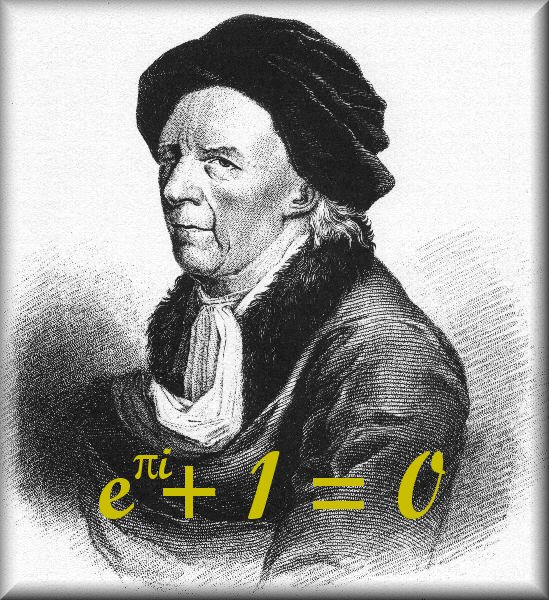
che è comunemente considerata uno dei più bei teoremi della matematica. Altri legami tra matematica e bellezza, che hanno giocato un ruolo prominente nella filosofia di Pitagora, si sono osservati disponendo i toni musicali in sequenze matematiche, che si ripetono ad intervalli regolari chiamati “ottave”. Una matematica di grande bellezza è la teoria dei numeri primi. Marcus de Sautoy12 descrive i numeri primi, gli oggetti più fondamentali della matematica nel seguente modo: “I numeri primi sono gli atomi dell’aritmetica. I numeri primi sono i gioielli incastonati nell’immensa distesa dei numeri, l’universo infinito che i matematici esplorano da secoli. Ai matematici i numeri primi infondono un senso di meraviglia: 2, 3, 5, 7, 11, 13, 19, 23,… numeri senza tempo che esistono in un modo indipendente dalla nostra realtà fisica. Sono un dono che la Natura ha fatto al matematico. La loro importanza per la matematica deriva dal fatto che hanno il potere di costruire tutti gli altri numeri. Ogni numero intero che non sia primo può essere costruito moltiplicando questi elementi di base primari. In una disciplina che si dedica a trovare andamenti regolari e ordine, i numeri primi presentano la sfida estrema. Provate ad esaminare un elenco di numeri primi. Scoprirete che è impossibile prevedere quando apparirà il successivo. L’elenco sembra caotico, casuale, e non fornisce alcun indizio riguardo al modo di determinare il suo prossimo elemento. Riuscire a trovare una formula che generi i numeri di questo elenco, una regola magica, è un problema che affligge la mente dei matematici da molti secoli” [16].
Sin dai tempi più antichi la “proporzione aurea“, rappresentata dalla lettera greca Φ, è considerata “bella” ed è stata presa in considerazione per ottenere una dimensione armonica delle cose. Riconosciuta come un rapporto esteticamente piacevole è stata poi usata come base per la composizione di quadri o di elementi architettonici [17]. Dalla geometria all’architettura, dalla pittura alla musica, fino alla natura del creato si può osservare come tale rappresentazione corrisponda ad un rapporto che è stato definito pari a 1,618…(numero d’oro). E’ stato anche dimostrato che la percezione umana mostra una naturale preferenza e predisposizione verso le proporzioni in accordo con la sezione aurea, i. e. la divisione di un segmento in due parti tali la parte maggiore sia medio proporzionale tra l’intero segmento e la parte minore. Gli artisti tenderebbero dunque, quasi inconsciamente, a disporre gli elementi di una composizione in base a tali rapporti. In questo contesto il matematico pisano Leonardo Fibonacci13, viene ricordato soprattutto per la sua celebre successione composta di una serie di numeri in cui ognuno di essi è la somma dei due numeri precedenti (0,1,1,2,3,5,8,13,21…). La “successione di Fibonacci” è una sequenza di cifre nascosta in molti fenomeni naturali che da oltre ottocento anni affascina i matematici. Johannes Kepler notò in seguito che facendo il rapporto fra due numeri di Fibonacci consecutivi, tale rapporto si avvicinava sempre più al rapporto aureo 1,61803. Allora la sequenza era conosciuta come la “divina proporzione” e veniva considerata quasi la chiave mistica dell’armonia nelle arti e nelle scienze. De “divina proporzione” è il titolo del trattato redatto dal matematico rinascimentale Luca Pacioli e illustrato da sessanta disegni di Leonardo da Vinci (1452-1519). Questo libro, pubblicato nel 1509, influenzò notevolmente artisti e architetti del tempo e delle epoche successive. Gli artisti e i matematici del Rinascimento tra cui Leonardo da Vinci, Piero della Francesca, Bernardino Luini e Sandro Botticelli rimasero molto affascinati dalla sezione aurea.
L’uso di figure geometriche si ritrova anche nei dipinti del pittore ottocentesco Piet Mondrian14, autore di numerosi quadri astratti.
Piet Mondrian

In questo quadro è ben visibile l’impostazione artistica dell’artista olandese che basa l’intero dipinto sull’accostamento di quadrati e rettangoli aurei.
Nell’opera dal titolo “La parade du cirque” il pittore divisionista francese Georges Seurat impiega varie sezioni aureealcune delle quali sono evidenziate nella figura.
Georges Seurat

Dunque possiamo incontrare la proporzione aurea nell’arte, per esempio nel famoso sorriso della Gioconda, o trovarla nella natura, per esempio nei petali delle rose e perfino nei bracci delle galassie a spirale.
La bellezza matematica nella natura
La bellezza matematica nella natura è stata studiata da Fibonacci, secondo il quale esiste una proporzione aurea che rappresenta la dimensione armonica nella natura, nell’arte (pittura e architettura), in astronomia e perfino negli uragani. La divina proporzione in natura si riscontra per esempio nelle conchiglie (Nautilus), dove si è notato chediversi tipi di conchiglie hanno una forma a spirale che si sviluppa secondo i numeri di Fibonacci.

Osservando attentamente il cielo notturno, nella globalità dell’infinito, s’individuano talvolta strutture dall’aspetto quasi nebulare: sono le Galassie. La Terra ed il Sistema Solare appartengono alla Galassia che prende il nome di Via Lattea che ha forma di spirale. Utilizzando un telescopio s’individuano in dettaglio differenti tipi morfologici di galassie ed in ognuno di essi variano le proporzioni dei componenti, le proprietà fisiche e quelle chimiche. Le galassie sono aggregati di stelle di massa e d’età diverse, di polvere cosmica e gas interstellare, principalmente idrogeno.
Le galassie

Il nucleo di questa Galassia ha un diametro di 80 anni luce e una luminosità pari a quella di cento milioni di volte il Sole. Si stima che l’età delle stelle sia all’incirca di 400 milioni d’anni. Si noti che mentre con uno dei bracci si collega ad una Galassia più piccola che appare come trainata, sembra ruotare come un ciclone terrestre in senso antiorario.
Sezione aurea di una galassia

L’uragano “Linda”, con venti che hanno soffiato a oltre 300 Km orari, colpendo la costa occidentale del Messico, è stato tra le tempeste più violente mai registrate nell’Oceano Pacifico.

La bellezza nella Botanica
In botanica quasi tutti i fiori hanno tre o cinque o otto o tredici o ventuno o trentaquattro o cinquantacinque o ottantanove petali: i gigli ne hanno tre, i ranuncoli cinque, il delphinium spesso ne ha otto, la calendula tredici, l’astroventuno, e le margherite di solito ne hanno trentaquattro o cinquantacinque o ottantanove.
I numeri di Fibonacci si trovano anche in fiori come il girasole. Infatti le piccole infiorescenze al centro del girasole sono disposte lungo due insiemi di spirali che girano rispettivamente in senso orario e antiorario. I pistilli sullecorolle dei fiori spesso sono messi secondo uno schema preciso formato da spirali il cui numero corrisponde ad uno della serie di Fibonacci. Di solito le spirali orientate in senso orario sono trentaquattro mentre quelle orientate in senso antiorario cinquantacinque (due numeri di Fibonacci); altre volte sono rispettivamente cinquantacinque e ottantanove, o ottantanove e centoquarantaquattro. Si tratta sempre di numeri di Fibonacci consecutivi. Le fogliesono disposte sui rami in modo tale da non coprirsi l’una con l’altra per permettere a ciascuna di esse di ricevere la luce del sole. Se prendiamo come punto di partenza la prima foglia di un ramo e si contano quante foglie ci sono fino a quella perfettamente allineata spesso viene un numero di Fibonacci e anche il numero di giri in senso orario o antiorario che si compiono per raggiungere tale foglia allineata dovrebbe essere un numero di Fibonacci.
Il Girasole comune è una pianta annuale appartenente alla famiglia delle Asteraceae, con una grande infiorescenza acapolino. La sistemazione dei fiori all’interno del disco avviene secondo la sezione aurea, ottenendo uno schema aspirali in cui il numero di spirali orarie e di quelle antiorarie sono successivi numeri di Fibonacci: di solito ci sono 34 spirali in un senso e 55 nell’altro e in girasoli molto grandi si possono trovare 89 spirali in un senso e 144 nell’altro.
Il girasole

Vengono in mente le parole del matematico Henri Poincaré sulla bellezza della natura: “Lo scienziato non studia la Natura perché è utile farlo, ma la studia per trarne diletto, e ne trae diletto perché la Natura è bella. Se non fosse bella, non varrebbe la pena di conoscerla, e se non valesse la pena di conoscere la Natura, la vita non sarebbe degna di essere vissuta” (!)
La bellezza nella Scienza
A questo punto, per amor di completezza, sembra opportuno fare anche un breve cenno alla bellezza nella scienza. Anche la scienza ha una sua estetica e bellezza. Purtroppo tutto questo non traspare spesso dal rapporto tra scienza e opinione pubblica, eccezion fatta per qualche programma culturale e scientifico in televisione e per alcuni articoli divulgativi sui quotidiani di maggior diffusione nella pagina della scienza. In realtà, gli scienziati dovrebbero migliorare la propria comunicazione col pubblico, promuovendo una migliore comprensione della scienza come fattore significativo del benessere di una nazione e dare il dovuto riconoscimento alla scienza anche come parte integrante della nostra cultura.
In questa visione i criteri estetici e quelli di bellezza e accuratezza possono trovare una nuova dimensione. Già il fisico teorico Paul Dirac, aveva dichiarato di essere sempre stato motivato nelle sue ricerche dal principio dellabellezza matematica, ed un altro grande scienziato, Henri Poincaré, parlando della bellezza della natura, aveva indicato la profonda motivazione che spinge lo scienziato a studiare i fenomeni naturali. Questa dimensione aveva peraltro le proprie radici negli stessi stili espositivi dei grandi scienziati. Quando il naturalista Buffon15 divenne membro dell’Accademia Francese, sorprese tutto l’uditorio col discorso pronunciato all’atto della sua nomina, un discorso che è rimasto celebre col nome di “Discours sur le style” (1753). Lo stile era la sua passione. Il suo discorso ebbe enorme successo e divenne un punto di riferimento per gli studenti francesi. Buffon vi sosteneva che solo lo stile poteva rendere comunicabile la conoscenza scientifica, a dispetto dell’inevitabile obsolescenza dei suoi contenuti. Solamente le opere scritte bene sarebbero riuscite a passare alla posterità. Sosteneva altresì che la quantità di conoscenze, la singolarità dei fatti, le stesse scoperte non avevano dentro di se la garanzia di essere immortali, ma che, se lo stile con cui erano esposte, era elevato, nobile e sublime, allora l’autore sarebbe stato ammirato per sempre, poiché solo la verità era durevole ed eterna. Aggiungeva anche che tutte queste cose – le nozioni, le scoperte, i fatti – erano esterne all’uomo, e che “Lo stile è l’uomo stesso”. Questo non va interpretato nel senso che lo stile riflette il carattere dell’autore, ma solo che gli permette di imprimere la propria impronta personale al pensiero espresso.
Osservazioni conclusive
Il percorso fin qui svolto ci ha avvicinato all’idea che una cosa che ci permette di guardare con fiducia e speranza il mondo in cui viviamo sia la bellezza che gli uomini di tanto in tanto sanno creare ed apprezzare. I quadri che dipingono, la musica che compongono, i libri che scrivono, la vita che vivono. Persino il gioco degli Scacchi e del Go, quando ne apprezziamo l’essenza, ci fanno penetrare nel mondo della bellezza.
Crediamo nell’aforisma di Fedor Dostoievskij: “La bellezza salverà il mondo”. E quando ci affacciamo al mondo, ci troviamo di fronte a un mondo sterminato, bello, complesso e iridescente. La sua bellezza ci emoziona e ci spinge ad indagarla. L’incertezza e la precarietà della nostra vita, che resta sospesa sull’abisso di ciò che non conosciamo, non la rendono insensata, ma solo più problematica e preziosa. Fra tutte, la cosa più ricca di bellezza è una vita bella. E’ questa l’opera d’arte più perfetta.
Ringraziamenti – Un sentito grazie a Nicoletta per una lettura critica del testo, la costante partecipazione e i vari chiarimenti in relazione alla cultura indiana. Molti ringraziamenti anche al Dott. Andrea Lauro per avermi introdotto all’affascinante gioco orientale del Go, e segnalato alcuni testi fondamentali (Kaoru Iwamoto, ”Go for Beginners” e Edward Lasker, “Go and Go-Moku”), oltre al CD-ROM “The Many Faces of Go” per apprendere questo gioco meraviglioso.
Note al testo
1.Marcel Duchamp (1887 – 1968) è stato un pittore, scultore e scacchista francese, naturalizzato statunitense nel1955. Considerato fra i più importanti e influenti artisti del XX secolo, nella sua lunga attività si era occupato di pittura, attraversando le correnti del fauvismo e del cubismo, diventando poi animatore del dadaismo e delsurrealismo. A partire dal 1923, Duchamp ha progressivamente diradato la sua produzione artistica per occuparsi quasi esclusivamente di scacchi, arrivando ad alti livelli. E’ anche stato capitano della squadra olimpica francese, nella quale giocava anche il campione del mondo Alexander Alekhine.
2. Paul Adrien Maurice Dirac (1902 – 1984), “Fellow” della “Royal Society” nel 1930, Professore di Matematica all’Università di Cambridge e Premio Nobel per la Fisica nel 1933, è famoso per aver pubblicato l’equazione relativistica per particelle a spin ½ nel 1928. Oltre all’unificazione delle teorie della Relatività Speciale e della Meccanica Quantistica, Dirac ha anche prodotto notevoli lavori sul monopolo magnetico e l’antimateria.
3. Bhagavadgita è il titolo di un poema epico-religioso indiano, contenuto nel più ampio poema della mitologia induista Mahabharata, che descrive la guerra tra i discendenti di Bharata, i cugini nemici Kaurava e Pandava (tramandato e scritto tra il V secolo a.C. e il III secolo d.C.).
4. Vasilij Vasil’evič Kandinskij (1866 – 1944) è un pittore russo, creatore della pittura astratta. Kandinskij nelle sue opere espone le sue teorie sull’uso del colore, intravedendo un nesso strettissimo tra opera d’arte e dimensione spirituale. Il colore può avere due possibili effetti sullo spettatore: un effetto fisico, superficiale e basato su sensazioni momentanee, determinato dalla registrazione da parte della retina di un colore piuttosto che di un altro e un effetto psichico dovuto alla vibrazione spirituale attraverso cui il colore raggiunge l’anima.
5. Godfrey Harold Hardy (1877 – 1947) matematico britannico e “Fellow” della “Royal Society”, è noto per i suoi contributi alla teoria dei numeri e all’analisi matematica. Il suo saggio “Apologia di un matematico” sull’estetica della matematica è considerato una delle migliori introspezioni nella mente di un matematico e una delle più riuscite descrizioni di cosa significhi essere un artista creativo.
6. Joseph Kling (1811 – 1910), è stato un problemista inglese, autore del libro”The Chess Euclid” (1849) che presenta 219 problemi. In collaborazione con Horwitz pubblicò nel 1851 “Chess Studies”, un classico sui finali.
7. Gerald Frank Anderson (1898 – 1983) è stato un compositore di scacchi e diplomatico britannico. Ha composto circa 500 problemi in due o tre mosse, molti dei quali sono considerati dei classici. E’ stato nominato arbitro internazionale per la composizione dalla FIDE nel 1960.
8. Samuel Loyd (1841 – 1911) è un pioniere della composizione ed è considerato il padre della scuola americana. Il suo primo problema fu pubblicato quando aveva solo 14 anni ed a 15 anni vinse il primo premio nel “Saturday Courier”. Nel 1878 aveva pubblicato il libro “Chess Strategy” contenente 500 problemi di scacchi. Le sue composizioni sono fantasiose, divertenti e difficile da risolvere.
9. Il pittore spagnolo Juan Gris [José Victoriano González] (1887 – 1927), nel periodo tra il 1914 ed il 1918, si era allontanato dal cubismo analitico per arrivare al cubismo sintetico, diventandone uno degli interpreti più interessanti. A differenza dei lavori dello stesso periodo di Picasso e di Braque, il cubismo di Juan Gris è animato da spirito scientifico e razionale, che lo porta verso un certo intellettualismo classicheggiante.
10. Si tratta della partita Keres – Eliskases (Semmering-Baden, 1937), un gambetto d’ala siciliano. La partita giocata in stile ipermoderno è la seguente: 1. e4 c5; 2. Cf3 d6; 3. b4 cxb4; 4. d4 Cf6; 5. Ad3 d5; 6. Cbd2 dxe4; 7. Cxe4 Cbd7; 8. Ceg5! Dc7; 9. c4 h6; 10. Ch3 g5; 11. Chg1 Ag7; 12. Ce2 e5; 13 Cg3. In tredici mosse, quando ancora non è stata ultimata l’apertura, il Bianco ha mosso il Cavallo di Donna ben sette volte (!), finendo tuttavia con un’evidente superiorità posizionale.
11. Sir Andrew John Wiles, (1953) è un matematico inglese, “Fellow” della “Royal Society” e Professore all’Università di Oxford. Specializzato nella teoria dei numeri è diventato famoso per aver dimostrato l’”Ultimo Teorema” di Fermat. Attualmente vive negli Stati Uniti ed insegna all’Università di Princeton
12. Marcus du Sautoy (1965) è un matematico inglese, Professore all’Università di Oxford. La sua area di specializzazione riguarda il campo della teoria analitica dei numeri e della teoria dei gruppi. Molto noto è il suo libro divulgativo “The Music of the Primes” del 2003. The Independent on Sunday lo ha definito uno dei maggiori scienziati del Regno Unito.
13. Leonardo Fibonacci era nato a Pisa intorno al 1170. Assieme al padre Guglielmo dei Bonacci, facoltoso mercante pisano, rappresentante della Repubblica di Pisa nella regione di Bugia in Cabilia (Algeria), aveva passato alcuni anni in quella città, dove aveva studiato i procedimenti aritmetici che gli studiosi maomettani stavano diffondendo nelle varie regioni del mondo arabo. Il suo testo “Liber abbaci” (Il libro del calcolo) è stato il più importante testo di aritmetica generale dell’Occidente, che ha insegnato a trasformare i complicatissimi calcoli con cifre romane in operazioni alla portata di tutti. Grazie al suo contributo alla fine del Cinquecento l’intera Europa aveva adottato il sistema indo-arabico.
14. Piet Mondrian [Pieter Cornelis Mondriaan] (1872 – 1944) è stato un pittore olandese e importante esponente del movimento artistico De Stijl. Nonostante siano molto famosi, anche se spesso imitati e banalizzati, i quadri di Mondrian dimostrano una complessità che smentisce la loro apparente semplicità. I quadri per cui è conosciuto e che consistono in forme rettangolari di rosso, giallo, blu o nero, sono il risultato di un’evoluzione stilistica proseguita nel corso di oltre trent’anni, continuando fino alla fine della sua vita.
15. George Louis Leclerc de Buffon (1707-1788) era stato un notevole matematico, ammesso all’Accademia delle Scienze a 26 anni. Dopo la nomina nel 1739 a curatore del “Jardin du Roi” (Jardin des Plantes) si era consacrato alla sua opera di naturalista, componendo nei successivi 40 anni i 36 volumi della sua ”Histoire Naturelle”.
Dal “Ritratto di Dorian Gray” di Oscar Wilde [1]:
“L’artista è il creatore di cose belle.
Rivelare l’arte e celare l’artista è il fine dell’arte.
Quelli che trovano significati brutti nelle cose belle sono corrotti senza essere affascinanti.
Questo è un difetto.
Quelli che trovano significati belli nelle cose belle sono colti.
Per loro c’è speranza.
Sono gli eletti per i quali le cose belle significano solo Bellezza.”
Bibliografia
[1] Oscar Wilde: “The Picture of Dorian Gray”, Collins, London and Glasgow, 1966
[2] David Shenk,:”Il Gioco Immortale”, Storia degli Scacchi, Oscar Mondadori, Milano, 2008
[3] Nicolas Giffard & Alain Biénabe: “Le Nouveau Guide des Echecs”, Bouquins, Paris, 2009
[4] Stephan Zweig: “Le joueur d’échecs”, Livre de Poche, 1993
[5] Isaak & Vadimir Linder : «Emanuel Lasker, 2nd World Chess Champion » Russel Enterprises, Milford USA, 2010
[6] Yasunari Kawabata: “Le Maitre ou le Tournoi de Go”, Livre de Poche, 1991
[7] Emanuel Lasker: “Lasker’s Manual of Chess”, Dover Publications, London 1932 & New York 1960
[8] Godfrey H. Hardy: “Apologia di un Matematico”, Garzanti, Milano, 2009
[9] Howard Staunton: “The Chess-Player’s Handbook”, London, 1847
[10] José R. Capablanca:”Chess Fundamentals”, G. Bell and Sons, London, 1968
[11] José R. Capablanca: “My Chess Career”, Dover Publications, Inc, New Yok 1966
[12] Richard Reti: “Modern Ideas in Chess”, Dover Publications, New York,1960
[13] Alexander Alekhine: “Gli Scacchi Ipermoderni”, Mursia, Milano, 2000
[14] Aleksei Suetin: “Das Schachgenie Paul Keres”, Sportverlag, Berlin, 1987
[15] Andrew Wiles: “La Teoria dei Numeri”, La Biblioteca di Repubblica, Milano, 2012
[16] Marcus de Sautoy: “L’Enigma dei Numeri Primi”, BUR Saggi, Milano, 2007
[17] Fernando Corbalàn: “La Sezione Aurea”, Mondo Matematico, Milano, 2011
Postfazione di Giangiuseppe Pili
Questo lungo saggio del professor Ivano E. Pollini tratta di un argomento a noi molto caro, la filosofia degli scacchi. La consonanza del saggio con Quadri in un’esposizione di Musorgskij è dovuta sia a ragioni strutturali che contenutistiche: dal punto di vista formale, un insieme di saggi intendono focalizzare un aspetto della bellezza da un peculiare punto di vista (gli scacchi, il go, la pittura, la matematica, la fisica etc.); da un punto di vista contenutistico, invece, il Concetto stesso della bellezza emerge per la sovrapposizione dei generi. Gli scacchi, in tutto questo, si mostrano sia come spunto, sia come essenza unificatrice dei vari aspetti singolari: gli scacchi si ritrovano in ogni sito dell’Impresa Umana, il particolare nel generale; da un altro lato gli scacchi si mostrano come emblema assoluto di ciò che può essere considerato bello al di là di ogni aspetto singolare, così essi ritornano come leitmotiv, il generale nel particolare.
La bellezza negli scacchi è il parallelo della bellezza del go e dell’arte e di molti aspetti meravigliosi della vita che Kant definì sublimi. Come diceva Lasker, ogni ambito della realtà implica lo scontro di forze contrapposte e il giudizio finale spetta alla prospettiva oggettiva di valutazione della qualità dello scontro. Gli scacchi sono intimamente lotta, al loro livello pratico, pragmatico e agonistico. Ma la profondità della mente spinge a vedere qualcosa di più profondo, che è l’intrinseca bellezza del concetto stesso dell’ordine, della piena pacificazione delle due parti. Il più profondo aspetto dell’articolo, a mio parere, sta proprio nel mostrare come la fuoriuscita dallo scontro sia, in una prospettiva più pacata e distaccata, oltre ogni aspetto emotivo istintivo che ce ne rende schiavi, l’arte stessa del trarre “il bello”, pacato, semplice e armonico oltre ogni scontro e ogni lotta. Per questo ambiti tanto diversi e concepibili separatamente (go, scacchi, arte, simbolismo, storia della cultura, fisica) mostrano tutti che l’unica “giustificazione morale” di ogni scontro sia proprio ciò che è il risultato estrinseco della lotta: l’intrinseca bellezza del risultato finale, come se fosse un che di non cercato ma di realmente unico. Per questo l’autore può concludere che: “Il percorso fin qui svolto ci ha avvicinato all’idea che una cosa che ci permette di guardare con fiducia e speranza il mondo in cui viviamo sia la bellezza che gli uomini di tanto in tanto sanno creare ed apprezzare”. Come diceva Wittgenstein, cito a memoria, “ciò che di più importante ho detto è tutto ciò che NON ho detto”. Questo vale per tutto ciò che I. E. Pollini ha lasciato intendere. E cioè che se c’è ancora una ragione ultima e definitiva per cui vale la pena giocare a scacchi, oltre ogni problema sociale, oltre ogni problema agonistico, cioè oltre ogni lotta, è proprio la loro intrinseca bellezza. Proprio come nella vita. E allora si comprende ancora di più in contro luce l’importanza della bellezza, proprio come simbolo del riscatto dell’uomo sulla barbarie che lo circonda ma che, se non ci fosse, potrebbe indirettamente rendere il mondo meno ricco di tutta la sua straordinaria bellezza.
Se questo è uno dei possibili significati profondi dell’articolo, non so dirlo. Ma è senz’altro uno degli aspetti che mi è sembrato importante sottolineare per mostrare quanto questo articolo non sia che la punta di un Iceberg del quale possiamo ammirare la lucentezza proprio per l’opacità del resto della vita.
Desidero ringraziare Ivano E. Pollini per averci gentilmente concesso di ripubblicare il suo bellissimo articolo. Sperando di poter ospitare altri suoi interventi, gli siamo grati per il suo meraviglioso e sorprendente lavoro.
In questa sede desideriamo ringraziare la redazione di Soloscacchi (http://soloscacchi.altervista.org/) che ci ha concesso con rapidità ed entusiasmo la possibilità di riportare l’articolo.
Riportiamo qui il link di riferimento: http://soloscacchi.altervista.org/?p=27833.




Mi sono permessa di postare nel mio blog questo articolo di grande interesse. Grazie per le pubblicazioni presenti in questo sito e il meraviglioso lavoro offerto.