Iscriviti alla Newsletter!
Il poligono di Cusano è un classico argomento della filosofia rinascimentale. L’autore suggerisce l’idea che la conoscenza umana sia limitata e non possa mai giungere all’infinito. La natura è infinita, dunque la comprensione dell’uomo non raggiungerà mai la pienezza della natura, sia del cosmo che del divino.
Questa concezione prende forma in una celebre immagine: il poligono inscritto in una circonferenza. Prendiamo che al principio ci sia un triangolo inscritto in una circonferenza, triangolo non perché il più perfetto delle spezzate chiuse quanto perché è la più piccola dei poligoni pensabili.
Immaginiamo di aggiungere un lato al triangolo: esso diventa un quadrilatero. Il perimetro del quadrilatero inscritto nella circonferenza è minore della circonferenza stessa.
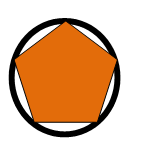
Allora, per giungere più vicino alla grandezza della circonferenza, supponiamo di aggiungere un altro segmento al poligono, che ora è un quadrilatero, e ottenere così un pentagono.
Ancora la grandezza della circonferenza è maggiore del pentagono. Se può non risultare chiaro attraverso il perimetro, si tenga conto che ad area maggiore corrisponde perimetro maggiore, così se due poligoni qualunque hanno diversa area, sarà maggiore l’area del poligono con il perimetro maggiore.
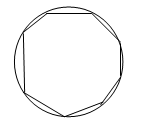
Se si procede con l’aggiunta di un segmento al poligono in modo da avere un poligono di n-lati, si osserverà che esso non arriverà mai a combaciare con la circonferenza giacché per quanto il numero “n” sia grande, esso sarà sempre e comunque inferiore alla grandezza della circonferenza in cui esso è inscritto.
Cusano con questa immagine fissa il suo punto nodale: la conoscenza umana non potrà mai giungere ad abbracciare l’interezza dei fenomeni naturali, ma solo e sempre di una parte, in questo senso, l’uomo è il poligono in continua crescita rispetto alla natura che è la circonferenza. Per Dio vale lo stesso discorso essendo egli un infinito in atto al pari della natura in cui l’uomo è inscritto.






Be First to Comment