Natural language and set theoretical and formal logic reductions – A philosophical account
A sheer love for propositions – An obsession with analytic philosophy, logics and mathematics
Analytic philosophy was born out of the general problem of solving metaphysics through a careful diagnostic of natural language. After the early days of formal logics and set theory with Boole and Cator, Frege and Russell arrived at the conclusion that natural language spontaneously produces irreducible paradoxes such as the liar and the sorites paradoxes. Through the length of these paradoxes, they concluded that traditional metaphysics was a gigantic mistake, formulable as it was under mistaken conception of language. The idea was ingenuous and simple to grasp. If I use very bad components and tools, I can only produce flawed engines, whose appearance is similar to a working engine until we check it. This ‘diagnostic’ approach to philosophy is as old as the Greeks, who were the first to outline different ways to ‘unveil life-threating mistakes through reasoning’. This was firstly tried in the realm of ethics, especially during the Alexandrine philosophies.[1] Wildly differently, this was tried again by the founding fathers of analytic philosophy.
Frege elaborated an entire philosophical system out of a new conception of logics applied to semantics through the instruments of the ‘new’ developments in formal logic, a Leibnizian ideal language through which all problems could be formulated and, then, solved by ‘brute force’ calculations.[2] In this broad category I am including set theory – in fact, it is arguable that formal logics and set theory cannot even be thought independently in the human mind.[3] In the following writing, I will consider set theory as the broad category including naïve set theory and Zermelo-Frankel theory plus the axiom of choice (ZFC).[4] It could be a matter of contentious, but set theory is, itself, a parallel endeavor that overlaps with the development of formal logic as we know. Moreover, set theory and formal logics are intended to mirror one another, where the sets are intended to be the object-domain of the propositions formulable in a formal language.[5] Set theory and formal logics tied together for solving all the natural language’s problems posed to human understanding, or so the founding fathers of analytic philosophy believed.
However, ironically, Russell himself formulated a paradox named out of his name, which destroyed the foundation of Frege’s project, apparently leaving the philosopher in disarray and never able to recover. It was then Russell’s turn. Alfred Whitehead and Russell started a colossal project, whose bravery is proved by its own length: four volumes of Principia Mathematica conceived to show how all mathematics can be ‘reduced’ to formal logic or, in other words, how everything that can be mathematically expressed is grounded on logics.[6] The project was worth trying, especially because it wasn’t me who had to do it.[7] In fact, ultimately, it was an endeavour intended to secure the foundation of mathematics from the paradoxes of natural language.
However, it was not intended for any specific, more practical endeavour, and it was mainly written in that same (natural) language intended to be defeated – which is, in itself, quite an interesting paradox. In fact, if any symbol has to be introduced in natural language first, and if any symbol is in fact a shortcut for a very long explanation which includes rules of interpretations and references to a domain of objects, it is absolutely unclear how the endeavor can even start.[8] How natural language could have succeeded in elaborating something that is considered better than itself? Why could we trust natural language when giving very complicated mathematical rules to create a full-fledge untested new language and distrust that same natural language when describing ordinary pieces of reality or philosophical ideas? Although in a far different way, this was how Wittgenstein tried to twist logics against itself in his post-Tractatus research.[9] However, as outlined elsewhere, Wittgenstein was still very fond of logics to go fully against it.[10] But for even more paradoxical reasons, the real vindication of natural language came partially through the purely syntactical conditions of formal logic itself that proved the intrinsic limitations of expressivity and coherence of any formal language sufficiently powerful.
Kurt Gödel paradoxical vindication
Kurt Gödel demonstrated that if any system comparable to the one formulated in the Principia Mathematica (namely, a logical formal language able to formulate and derive through rules well-defined propositions about arithmetic) is coherent, then it must be incomplete.[11] Let’s assume a formal language L and a system of rules S expressed in L. Let’s assume that L has the capacity to express propositions about arithmetic, then there must be a proposition G expressed in L such that if G is provable, then L is inconsistent. If G is formulable in L but it cannot be either proved G nor not-G, then L can be consistent, but it is incomplete (as it cannot prove all the propositions formulable). Therefore, if L is consistent, it cannot be complete and if it is complete, it is because it is inconsistent. In fact, if L is complete, it must be because there is a contradiction (falsehood) within it and, as such, it trivializes the system. This is, for a layman like me, the main take away out of a very dense logical proof readable only by hardcore logicians (if any). In (historical) conclusion, all the previous founding fathers of analytic philosophy were proved wrong and natural language is still there with all of us.
Notably, in Godel’s formulation of his two theorems (whose results were those presented) truth was ‘reduced’ to a syntactical notion of general non-contradiction within a system, namely the capacity of a logical system S expressed in a given language L to not allow the co-existence (provability) of both p and not-p.[12] This is considered a specific reduced syntactical way to treat contradiction, staying away from any ‘stronger’ semantical understanding of truth-value. Once got the contradiction, all the system collapses given the interpretation of the modus ponens under the classic interpretation of the implication operator (if… then…) in classical terms, intended to be as strong as permitting any conclusion from assumed false premises (meaning, if I assume or prove a proposition a as false, I can imply anything out of a: any material conditional is true if the antecedent is false). This makes sense, as this is the minimal requirement for something to make sense, and once accepted a nonsense, one can say anything.[13] This syntactical notion of truth is quite limited in scope as it does not involve any meaning or reference to any extra-linguistic reality, but only to the sheer derivability of two independent propositions (G and not-G) out of the same system of rules. From this point on, everything is left to formal logics and to the different logical system that tries to explore different operations, operators, languages, and rules.
Apparently, however, the syntactic notion(s) of truth are not enough to account for what we express through natural language. In fact, they are far from it. For instance, if we say ‘The language L contains a proposition G such that G is formulable and it cannot be demonstrated within L rules and axioms, hence G cannot be either true or false. We know G to be true, hence G is true in spite of its being unprovable.’ This sentence about L can be understood only assuming a wider notion of truth – in fact, a non-merely L-syntactical reduction to provability within L. Even somebody who does not know or understand much about formal logic would be able to grasp the meaning of the statement and, with it, its truth-conditions. This is already a proof of the fact that something stronger than pure syntactical notions of truth must be in place. But there is more. If we delve into the nature of G, we could not express anything about it within L, exactly because G cannot be either proved true or false. To say it differently, G and its negation not-G cannot be recursively produced by L with its language and rules. Asking the truth-value about G or not-G can only be asked through a non-syntactical question, which, in turn, must be in natural language.[14] Hence, again, although portions of argumentation can be reduced to merely syntactical notions, the very fact that they are formulable is intrinsically depending on a broader landscape of meanings. And this landscape is given to us through natural language. I would argue that this is how mathematical Platonism can be understood – that is the philosophical standing for more than what is just mechanically produced through any possible device.[15]
Let’s go beyond the boundaries of what can be proved, shall we?
For these reasons, philosophers found logics and set theory too strict or too limited for their more grandiose aspirations. Different versions of truth can be elaborated, but they could converge with the conception of having two different levels from which deriving a judgement: a given proposition, well formulated within a given language L, could be true or false depending on its relation to something external to it, a domain of objects where the proposition is interpreted. Assuming a as formulated in Lm, where Lm usually refers to mathematical objects (e.g. numbers), a is true if and only if there is a certain mathematical object that stands in a given situation (e.g. the mathematical object does entertain a certain relation with another mathematical object). Otherwise, the proposition a is false.
The clearly flimsy notion here is ‘interpretation’ or how two different things are associated together through what rule. For instance, a proposition as R(#,*) could state that two mathematical objects, a and b stand in a given relation R and if that is the case, than R(#,*) = True. However, why or what should limit our imagination, thinking that # and * are in fact two mathematical object? Is there any necessary principle that guide us in the interpretation of those symbols? No, there is not. In fact, we can have multiple domains of interpretation and the propositions should still old: independently of any domain, the form of the propositions alone could safeguard their overall truth-value.[16] In fact, as we have seen, formal logics (first order formal logics and set theory – to give more specifications) was intended to save the world from the catastrophe of confusion and misunderstanding. Therefore, the idea was to rescue it from any meaning whatsoever, a pure structure out of which truth is preserved. But truth in this semantic sense requires something more and, after all, we want to give a meaning to our language: set theory is a construction out of the empty set, which seems to be a bit too empty for our ordinary life. Then, the idea was, until everything can be expressed in the similar fashion than set theory, we are safe enough.
All said so far is only a tedious window on something important for our purposes: the obsession for propositions and their truth-value, and their fundamental place in the history of logics, set theory, and semantics (philosophy of language). The obsession is based on something quite important, which is the minimal unity that could be judged as true or false. ‘George’, ‘cat’, ‘red’, ‘bigger than’, ‘equal’ are all words whose truth-value is informulable exactly because is predicated of them or predicated by them. At the same time the objects ‘GEORGE’, ‘CAT’ or the color ‘RED’, in capital letters to underline their external-to-language nature are neither true nor false. Objects can exist, but they cannot be technically true or false. Only the predication, the linguistic reunification between a subjective identification (name or descriptions, anything that can ‘uniquely’ identify something existing – or not existing) can yield a truth-judgement. As a result, both philosophers, logicians and mathematicians are all obsessed by propositions and different conceptions of truth. Reasonable, so far so good. However, much of recent understanding of an entire conception of analytic philosophy inherited the same obsession for mathematical propositions (as it was entirely founded out of those notions).
Philosophers’ and mathematicians’ obsessions for their beloved formal propositions curtail them to see better how incredibly efficient natural language is from a logical point of view. In essence, this analysis is about understanding how natural language is in fact incredibly powerful when it comes to expressivity and capacity to represent reality under the very lenses of logic plus set theory. However, for seeing the point, it was requested to understand the discrepancy between provability and truth (however understood),[17] and why there is this deep infatuation for ‘pure syntax’. As a result, philosophers tried to reduce portions of natural language to simplified, formal components of it (logics, plural) without realizing that natural language is still the place where everything starts and where everything is still more efficiently expressed.[18]
The unorthodox Ludvig Wittgenstein is any different
Ludvig Wittgenstein was firstly obsessed by logics and set theory as anybody else.[19] Moreover, his ignorance of (basically) all history of philosophy allowed him to join the newborn Frege’s and Russell’s logicist foundational projects (more the former than the latter) of analytic philosophy without any further ado. In fact, he produced the Tractatus Logico-Philosophicus in which, essentially, he arrived to claim that everything that is not formulable within the strict limits of what can be said (by – simplifying – set theory and logics), it is nonsense.[20] Maybe it was a useful and unavoidable nonsense, but still a nonsense, strictly speaking. The notion of nonsensicality, if anything of the sort exists, is what cannot be predicated as true or false, but it can be, nonetheless, formulable through natural language. In his early vision, anything scientific could be in principle expressed in these terms.[21] Then, again, the obsession of the proposition is apparent. It dominates the scene and, as a matter of fact, it is the clearest notion in Wittgenstein’s early thought, as what is behind or beneath language (states of affairs and facts – his metaphysics) is not as clear.[22]
However, although convinced to have solved all the problems of philosophy (after all, why not?), Wittgenstein drastically changed his mind in his conception of language.[23] The second part of his thought is aimed to show how nobody can claim that there is a primordial ‘logical’ language, able to solve all we want to express. His philosophy of mathematics is a gigantic series of sparse thoughts united by the sheer diversity of views on the same topic (mathematics and what we can express through language).[24] And he concludes that, essentially, natural language baffles both formal logics and set theory (but not science, as it is often described in natural language and in fact it goes beyond both logics and set theory). In this renewed interest for diverse forms of expressions, Wittgenstein is less obsessed by propositions, but not necessarily less concerned about truth, as he wants to show that competing visions of truths coexist within natural language. This is not the place to explore more than what already introduced, but it is telling of the fact that all the different schools of thought in analytic philosophy are based on a common vision, even when differently stated: propositions are the building blocks of our language and, as such, of our semantics and our understanding of truth. No propositions, no truth, no party.
Moving a little away from the sheer love for propositions and truth-values
I share all the idiosyncrasies of analytic philosophy. Although not as strong in pure formal calculus – which apparently is not easy to fathom for anyone,[25] I spent years in studying all the foundations of analytic philosophy (set theory, formal logics and mathematics) and my mind is still engrained in those concepts, operators, operations, and languages. I can even claim that those studies allowed me to be the human being I am saving myself an infinite amount of times, and even finding a job as an analyst (no, it is not all that bad).
Truth is my main core value, as it stands beyond everything, and it is adamantly careless about our limited moral, and partisan feelings for survival. It is the purity of the God that does not care, truth is the simplicity of the sheer existence. Truth, whatever it is, is fundamental and, in fact, my philosophical vision – failed in popularity as it is! – is labelled as ‘theory of eternal truths’ or ‘eternal truth theory’,[26] which assumes human history as a persistent (re)formulation of constant statements about the world whose meaning is tied by the world by the rules of language. For the very same reason, I was (I am) obsessed by propositions and how to express truth and how those strings of symbols connect to the world. I am, after all, an analytic philosopher.
However, I recently arrived at new discoveries that I found as important as unconsidered because they depend on how the natural language works and expresses the world. From the propositions back to more fundamental components but with a constant eye to the truth. What I mean is that I consider natural language to be the ultimate source for any more specific slicing over different species of arguments and their differential rendering. What strikes of natural language is its capacity to be able to express so many different types of arguments, from one side, and its impressive architecture and descriptive power. Essentially, a linear coded way to express a given well-formulated proposition is, in fact, capable of rendering incredibly diverse types of objects in all possible dimension (time and space). Let’s take an example as a starting point.
[1] There is a notebook and a pen on the table.
This sentence can be totally reformulated within a set of sentences in principle reducible to formal logics and set theory. I will follow a traditional notation:[27]
[SK1] Start
[1.0] Assuming that there is a set of given physical objects =
∀S ∀O {a ∈ O ∧ O ⊂ S}
[1.1] There are tables = ∃!T {a ∈ T | T(x)}
[1.1.1] Of all the tables, this is the one (ostensive identification)
∀(x) ∃!t {t ∈ T | T(x)}
[1.2] There are notebooks = ∃!N {b ∈ N | N(x)}
[1.2.1] Of all the notebooks, this is one = ∀(x) ∃!n {n ∈ N | N(x)}
[1.3] There are pens = ∃!Pn {c ∈ Pn | Pn(x)}
[1.3.1] Of all the pens, this is one = ∀(x) ∃!pn {pn ∈ Pn | Pn(x)}
[1.4] Tables, pens, notebooks can stand in given spatial relations that could be described in geometrical terms, such that the following statements could be either true or false:
[1.4.1] The given pen is on the table = ∃!t ∃!pn R1(t,pn)
[1.4.2] The given notebook is on the table ∃!t ∃!n R1(t,n)
[1.4.3] There is a set of relations between the pen, the notebook and the table = ∃!t ∃!n ∃!p R2(p,t,n)
[1.4.4] R1 ≠ R2
—
[1.4.5] ∃!n ∃!p R3(p,n)
[SK1] End
Where Rs should be characterized in specific geometrical terms. Notably, R1 ≠ R2 ≠ R3 (which makes sense as the pen and the notebook are in a different geospatial relation between themselves, where they entertain the same relation with the table). as well as must be assumed different, for obvious reasons. From here we can then draw the merely set theory scheme
[SK2] Start
[1.0] ∀S ∀O {a ∈ O ∧ O ⊂ S}
[1.1] ∃!T {a ∈ T | T(x)} ∧ ∀(x) ∃!t {t ∈ T | T(x)}
[1.2] ∃!N {b ∈ N | N(x)} ∧ ∀(x) ∃!n {n ∈ N | N(x)}
[1.3] ∃!Pn {c ∈ Pn | Pn(x)} ∧ ∀(x) ∃!pn {pn ∈ Pn | Pn(x)}
[1.4] [1.4.1] ∧ [1.4.2] ∧ [1.4.3] /
[1.4.1] ∃!t ∃!pn R(t,pn)
[1.4.2] ∃!t ∃!n R(t,n)
[1.4.3] ∃!t ∃!n ∃!p R(p,t,n)
[1.4.4] R1 ≠ R2
—
[1.4.5] ∃!n ∃!p R3(p,n) From [1.4.3] and [1.4.3] (simplified)
[SK2] End
This is a possible set theoretical reduction of a sentence of ten words of which one verb and three category names used as instances for specific objects. This seems to be very remarkable. To reduce natural language on mere set theoretical syntax and argumentation (as there is a deduction), it took 4 propositions and then other five sub-propositions, which breakdown the most complicated relation into multiple relations. In spite of the called ‘vagueness’, natural language is capable of describing the world in quite shorter, even elegant way.
Moreover, it must be conceded that even if a speaker of English does not do as much calculation in his/her mind when reading the sentence, it must be assumed that he/she is fully able to understand its truth-conditions, as this was famously Wittgenstein’s requirement for what it means to understand a proposition. If this is the case, then the random English speaker must be assumed capable of expressing what contained in [SK2]. It does not seem quite an achievement or something difficult only because it is so natural that we don’t realize how complicated this operation must be and how fast it is performed by the mind through the brain. It is in fact remarkable that so much information is contained in such a tiny space. As a result, we discovered that a single sentence without any complicated clause would require an impressive re-writing for being ‘reduced’ to set theory and formal logic expressions. In fact, a single sentence is not an argument (although as in SK2 [1.4.5] infinite conclusions can be drawn, some trivial but some remarkable).
Before moving on, it must be appreciated that the proposition [1] has also an important metaphysical assumption that cannot be entirely reduced in set theoretical language as partially tried in [1.0]: what is requested is that those objects identified in the sentence are ‘existing’ into what could be called ‘reality’, whatever the notion of it could be. This means that there is a clear commitment over the specific truth-conditions over that sentence, that cannot be only regarded as set theoretical, and they assume some appreciation of this specific possible world and its physical laws (e.g. a world in which gravity would not exist, there could not be any situation in which [1] could be true or even formulable). In fact, set theory was assumed capable to describe anything, although its primary aim was to grant the foundation of mathematics. However, how can a metaphysical statement such as this could be introduced in set theory? Set theory does not have the language for saying ‘this pen is not just an item among the set of all pens, it is a particular entity that in fact is in the world’. There is no such capacity, as the language required to express it would go far beyond the empty set and all the possible operations on it. As a result, set theory is unable to distinguish the numbers of unicorns and the numbers of apples (that is: it can count stuff, but it cannot say what is real stuff and what not). However, this metaphysical requirement is minimal, in a sense, as it does not commit to any specific metaphysics – however, as it is clear, assumptions are made over the world in which that sentence makes sense (as already proved).
Now we grasped how rich and complicated is a single sentence of natural language if reduced to set theoretical statements and formal logic structure of argumentation. Now let’s consider how natural language is in fact able to produce such a miracle.
Is it really a miracle? – Deconstructing a proposition in natural language
Obviously, there are no miracles, but the capacity of natural language to do so much (set theoretical) work with so little is a major wonder to my mind. Let’s go back to our sentence:
[1] There is a notebook and a pen on the table.
‘There is a…’ counts both as a metaphysical statement (there is something existing somewhere in the universe [SK2][1.0] plus explanations) and a set theoretical quantifier ([SK2][1.1]-[1.3]). Obviously, these two ‘functions’ are of different nature, but both rest their weight on the same pillar (‘There is a…’). In reality, this ‘there is a…’ is also a georeferential indicator, as ‘is’ here is both asserting the existence of several relations attributed to the things that follow, and simultaneously qualifying the nature of those relations as spatial.[28]
Moving on, the logical operator ‘and’ is creating a relation between the set of notebooks and pens such that it pairs two of their items (‘that specific pen’, ‘that specific notebook’). This use of ‘and’ could be stated as not ‘logical’ in nature, strictly speaking, but only set theoretical. However, as it is seen by [SK2][1.2]&[SK2][1.3], this ‘and’ is avoiding the formulation of two different propositions: ‘There is a notebook. There is a pen.’, where the joint is created between the two sets pairing the elements, which are then immediately related to a third. In this sense, this ‘and’ is doing a significant work: it is saving space in identifying the pair of objects of two different sets and it is also sparing the segmentation of the message in multiple sentences, then used as a formal operator.
From a logical perspective, there could be an ambiguity in the use of ‘a notebook’ and ‘a pen’, as they stand for ‘at least one item of the set of pens’ (etc.). However, it is arguable that in the majority of cases, the interpretation of [1] would be clearly driven by an ostensive or even more intuitive way to identify the corresponding objects in the piece of reality described (that’s why we used ‘∃!N’ instead of ‘∃n N(x)’ to denote ‘a notebook’. Finally, probably the most remarkable piece of all the propositions here is the geometrical relation introduced by the ‘on’. This ‘on’ is bearing the weight of the spatial relations among: ‘notebook’, ‘pen’, and ‘table’. This is proved by the fact that the following statements are both true: ‘There is a notebook on the table’, ‘There is a pen on the table’. Moreover, this ‘on’ is introducing a specific spatial relation as it is quite clear where the notebook and the pen are on the table: on the top. Interestingly, this seems to be almost obvious for any English speaker, as there are no other ways in which the notebook and the pen can stay on the table, but this also shows how natural language, and its interpretation heavily relies on physical notions that are behind the strict interpretation of the terms.
Deconstructing a slightly more convoluted proposition in natural language
The ‘simple’ sentence [1] has done its work and it is time to explore something more convoluted: a proposition with multiple clauses.
[2] In the second century of the Christian Aera, the empire of Rome comprehended the fairest part of the earth, and the most civilized portion of mankind.
Let’s start with an informal breakdown:
[SK3] Start
[2.0] Assuming that
[2.0.1] there is a set of given physical objects,
∀S ∀PHY_O {a ∈ PHY_O ∧ PHY_O ⊂ S}
[2.0.2] assuming that there is a set of given social objects
∀S ∀SOC_O {b ∈ SOC_O ∧ SOC_O ⊂ S}
[2.0.3] assuming that [2.0.2]≠[2.0.3] = PhyO ≠ Soc_O
[2.0.3] assuming that there is a conventional set of time events,[29]
∀S ∀TM {c ∈ TM ∧ TM ⊂ S}
[2.0.4] PHY_O ≠ SOC_O ≠ TM
[2.1] There is the set of centuries = ∃!Tm ∃CEN {cen ∈ CEN ∧ CEN ⊂ Tm}
[2.2] There is the set of Aeras = ∃!Tm ∃AER {aeras ∈ AER ∧ C ⊂ AER ⊂ Tm}
[2.3] [2.1] is a subset of [2.2] is a subset of [2.0.3]
∃!TM, ∃AER, ∃CEN {C ⊂ Aer ⊂ Tm}
[2.4] There is the set of empires
∀SOC_O ∃EMP {emp ∈ EMP ∧ EMP ⊂ SOC_O}
[2.4.1] There is one specific item of [2.4] identified as ‘empire of Rome’
∀SOC_O ∃EMP {empire_of_rome ∈ EMP ∧ [∀x ∈ EMP empire_of_rome ≠ x EMP(x)] ∧ EMP ⊂ SOC_O}
[2.5] There is the earth = ∀PHY_O ∀EAR {e ∈ EAR ∧ EAR ⊂ SOC_O}
[2.5.1] The earth is subdivided in parts
∃EAR ∃(x){e ∈ EAR ∧ Part(x)}
[2.5.2] There is a property ‘Fair’ that is predicated of [2.5.1].
∃EAR ∃(x){e ∈ EAR ∧ Fair(x)}
[2.6] There is the set of mankind =
∀PHY_O ∀SOC_O ∀MNK {f ∈ MNK ∧ MNK ⊂ SOC_O ∧ MNK ⊂ PHY_O}
[2.6.1] There is the property ‘civilized’ that is predicated of [2.6],
∃MNK ∃(x){f ∈ MNK ∧ Civilized(x)}
[2.7] There are several different relations between ‘the empire of Rome’, ‘the fairest part of the earth’, ‘mankind’.
[2.7.1] The ‘fairest part of the earth’ is included in ‘the empire of Rome’,
∃EAR ∃EMP ∃!(y) ∃(x) {e ∈ EAR ∧ Part(x) ∧ Fair(x) | y = ‘empire of Rome’, e ∈ ‘empire of Rome’}
[2.7.2] The ‘most civilized portion of mankind’ is included in ‘the empire of Rome’,
∃MNK ∃EMP ∃!(y) ∃(x) {f ∈ MNK ∧ Civilized(x) | y = ‘empire of Rome’, f ∈ ‘empire of Rome’}
[2.7.3] [2.7.1] and [2.7.2] are elements of the set of time events named ‘the second century of the Christian Aera’.
CEN{…, [2.7.1],[2.7.2],…}
[SK3] End.
Before giving the fully formalized set theoretical description of [2], it is important to notice how insufficient are the descriptions of the assumptions from a metaphysical point of view. Social objects, physical objects and time events are all very structured events. Even the simplest of the three (conventional time), the easiest to formalize in set theoretical terms using ℕ (natural numbers) as generic sequence for mimic time, requires much more work to be fully described in set theoretical terms. Much worst is the structured order of physical objects (particles, atoms, molecules etc.) and social objects (citizens, agreements, institutions, etc.). Not only the technical work would be so daunting be probably worthless[30] (although not as daunting as reading the uselessly lengthy A Theory of Justice), but it would certainly be unable to do the job we are asking of it. Meaning, if the goal of a set theoretical and logical rendering would be to cut the Gordian knot of the vagueness and ambiguity of natural language, this endeavor is immediately ruled out. Let’s consider two examples here:
[2.0.1] there is a set of given physical objects,
∀S ∀PHY_O {a ∈ PHY_O ∧ PHY_O ⊂ S}
[2.0.2] assuming that there is a set of given social objects
∀S ∀SOC_O {b ∈ SOC_O ∧ SOC_O ⊂ S}
In [2.0.1] and [2.0.2] social objects are disjointed by physical objects, although both are part of the S, which is intended to be the arbitrary set that includes all our sets (something like the full domain of all possible predicated objects, items, whatever…). This subdivision makes sense on an ordinary level, without specific metaphysical commitments. However, it should be apparent that there will be philosophers outraged by the fact that social objects are not considered as a subset of the physical objects.
For instance, John Searle tried to keep both positions, defending a ‘naturalized social ontology’, which would turn any social object in a particular, very complicated physical object.[31] However, there is a clear sense in which a social object stands out merely physicalistic ontologies. In fact, on a merely practical perspective, there is no need to think about contracts as made of particles: would it be explicatively important? Not to the bureaucrat who has to sign it. In fact, the act of ‘sign’, though technically physical in nature, has its meaning because of the physically-independent function is playing. As a result, when we deal with human history in general, the descriptions about the physical world are less detailed than the general conditions for human action. Anyway, this should give a sense of the troubles that would be just put under the rug in trying to use innocent set theoretical and logic accounts of reality. A lot of implicit structure is put on those light things called set and they are not able to sustain the weight of reality unless major work is done, a work that would just be as controversial as any other natural language description or metaphysical account of reality.
This discussion should show why Barry Smith and others tried to remark how far set theory is from formal ontology, which is based on a neo-realist Aristotelian account of reality. According to formal ontologists, reality has a unique structure that can be enforced to language in a way that (mainly natural) language can model reality efficiently. It could be the case that this endeavor overlook other problematic aspects of natural language, but it is a clear reply to the insufficiency of logic and set theory vis a vis the richness of natural language.
Quite tellingly, [2] is a quotation from Decline and Fall of the Roman Empire of Edward Gibbon. As it should be clear, if only a sentence of a three-volume publication requires eight different propositions plus twelve subclauses and assumptions, it is quite clear that natural language does a quite elegant work in rendering reality at least under hypothetical considerations over its capacity to make it. Now let’s turn to the next schema. From [SK3] we can obtain [SK4]:
[SK4] Start
[2.0] Assuming that
[2.0.1] ∀S ∀PHY_O {a ∈ PHY_O ∧ PHY_O ⊂ S}
[2.0.2] ∀S ∀SOC_O {b ∈ SOC_O ∧ SOC_O ⊂ S}
[2.0.3] [2.0.2]≠[2.0.3] = PhyO ≠ Soc_O
[2.0.3] ∀S ∀TM {c ∈ TM ∧ TM ⊂ S}
[2.0.4] PHY_O ≠ SOC_O ≠ TM
[2.1] ∃!Tm ∃CEN {cen ∈ CEN ∧ CEN ⊂ Tm}
[2.2] ∃!Tm ∃AER {aeras ∈ AER ∧ C ⊂ AER ⊂ Tm}
[2.3] [2.1] ⊂ [2.2] ⊂ [2.0.3] / ∃!TM, ∃AER, ∃CEN {C ⊂ Aer ⊂ Tm}
[2.4] ∀SOC_O ∃EMP {emp ∈ EMP ∧ EMP ⊂ SOC_O}
[2.4.1] ∀SOC_O ∃EMP {empire_of_rome ∈ EMP ∧ [∀x ∈ EMP empire_of_rome ≠ x EMP(x)] ∧ EMP ⊂ SOC_O}
[2.5] ∀PHY_O ∀EAR {e ∈ EAR ∧ EAR ⊂ SOC_O}
[2.5.1] ∃EAR ∃(x){e ∈ EAR ∧ Part(x)}
[2.5.2] ∃EAR ∃(x){e ∈ EAR ∧ Fair(x)}
[2.6] ∀PHY_O ∀SOC_O ∀MNK {f ∈ MNK ∧ MNK ⊂ SOC_O ∧ MNK ⊂ PHY_O}
[2.6.1] ∃MNK ∃(x){f ∈ MNK ∧ Civilized(x)}
[2.7] /
[2.7.1] ∃EAR ∃EMP ∃!(y) ∃(x) {e ∈ EAR ∧ Part(x) ∧ Fair(x) | y = ‘empire of Rome’, e ∈ ‘empire of Rome’}
[2.7.2] ∃MNK ∃EMP ∃!(y) ∃(x) {f ∈ MNK ∧ Civilized(x) | y = ‘empire of Rome’, f ∈ ‘empire of Rome’}
[2.7.3] CEN{…, [2.7.1],[2.7.2],…}
[SK4] End.
The explication of the single statements was given in [SK3] and I won’t go back to them. However, it is important to remark one feature of [SK4]. [SK4] show the ‘implicit’ truth conditions of the propositions in natural language in [2] and refined in [SK3]. If so, this is another sign of the ‘miracle’ we already introduced before, meaning we need to assume that the reader is able to grasp all of them, as otherwise he/she wouldn’t be able to understand [2], as Wittgenstein asked. At least implicitly, the reader must be assumed capable of figuring the set theoretical and logical requirements of [2] and checking all those conditions to understand if that could be the case or not.
Interestingly, [2] does not add at the end ‘and this is what happened in the universe’ or something equivalent, but it clearly must be intended in that way. As the excerpt was taken from a history book, any sentence of the book is conditionally judged in function of their relation to reality (where, for instance, a fiction book would not). Hence, we need to believe that each sentence was the result of a proposition formed by the author to convey a truthful depiction of reality. In other words, we need to assume that the proposition is true and believed as true, ceteris paribus. However, as just stated, there is added level of flexibility of natural language to allow both interpretation of statements as the same proposition could be written in two different contexts and being clearly true or false depending on the situation (e.g. [2] written in a history book receives a different conditional truth-value than if it was written in a fictional book, where it would be strictu sensu false by definition).
As in the deflationist accounts of truth, natural language usually presupposes that if p is stated, then ‘p is true’ when ‘p’ is stated under ordinary circumstances for describing something about (present or past) reality. This not a unique feature of truth-values. As argued elsewhere, any ordinary statement has an implicit timestamp that is usually grasped implicitly, although possibly introduced by time tenses in the verb. For instance, making sense of [1] ‘There is a notebook and a pen on the table’ implicitly assumes ‘[1] is true at time t’ where ‘time t’ is assumed to be the time of when [1] was stated. In fact, only logicians are able to think about [1] as a-temporal. The present tense is ambiguous in the sense that can be used for generalization over time (such as ‘gravity forces things toward the center of the Earth’) but also for events that are currently the case such as [1]. Let’s turn now to [2] to see how natural language is able to perform all the logical and set theoretical operations reported in [SK4].
[2] In the second century of the Christian Aera, the empire of Rome comprehended the fairest part of the earth, and the most civilized portion of mankind.
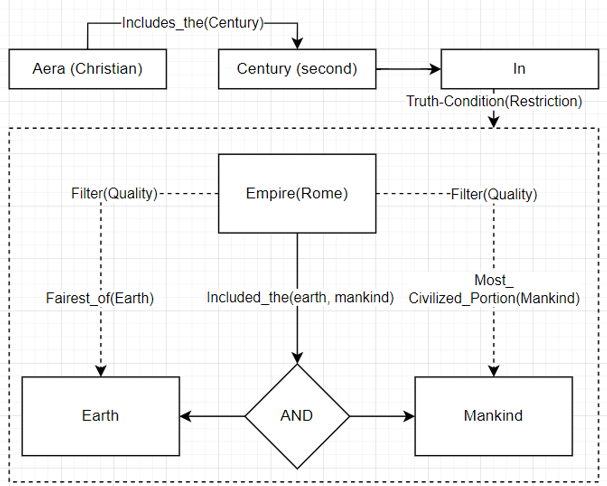
The proposition starts with immediately operating a reduction over the time frame, which runs as a filter over the following sets of objects (which means that those sets include different items over time). ‘In the second century of the Chirstian Aera’ does a lot of work in two different ways. First, ‘the second century’ implies that there are things called ‘centuries’ and these things are ordered such that there is only one ‘second century’, as indicated by ‘the’. Second, ‘of the Christian Aera’ is appended to ‘second century’, as it operates as second restriction over the time conventions and, again, it is saying ‘there are different Aeras, and we are considering the second’. The ‘of’ is the way in which natural language creates a specification over the set of centuries establishing a clear relation of belonging between centuries and aeras such that ‘aeras’ are sets of ‘centuries’.
All this work is done by a single ‘of’ plus ‘the’ and ‘second’. The specification over the Aeras is done by the adjective ‘Christian’, which here I consider just as a placeholder for a time convention that must be understood and known by the reader (I am sure different readers would appreciate this time conventions differently!). The initial ‘in’ is doing an important work. It is used as if time was a space, as it is indicating that something is happening within a given ‘space of events’. This is proved by the fact that ‘In’ here is intended as ‘Inside’, which usually intended as a space. So, ‘In the second century…’ is saying ‘There is something happening in this given time frame:…’. This inclusion over what is following is given by the initial ‘In’ which saves a lot of space in terms of sheer number of words and implicit rules.
Moving ahead, ‘the empire of Rome’ is another restriction over the set of ‘empires’ as it is saying both that ‘there are empires, and a unique item is ‘the empire of Rome’’. The specification over the set of empires is given by ‘of’, which is again appended to the name of the general category of things we are considering. Then, the relation between ‘the empire of Rome’ and what follows is introduced by the verb ‘comprehend’ that refers to two distinctive propositions. ‘Comprehended’ relates ‘the empire of Rome’ with the immediately subsequent object ‘the fairest part of the earth’. However, it simultaneously relates ‘the empire of Rome’ with ‘the most civilized portion of mankind’. It does so through the ‘and’ that is used as a shortcut for ‘the empire of Rome comprehended’.
In this case, again, ‘and’ is used in two distinct ways: logical operator and shortcut. This saves five words and one distinctive sentence! ‘the fairest part of the earth’ is another specification over the partition (assumed here essentially arbitrary) of the earth. This is done, again, by ‘of’. However ‘the fairest part of’ restricts ‘the earth’ in saying that there is a subset of earth such as what is included into it is a part of a whole (earth) and that this is qualified as ‘the fairest’. Notably, the ‘part of’ here is clearly a topologico-mereological feature attributed to the earth, which implies a specific operation which is not technically part of set theory.[32]
‘the fairest’ implies the presence of an order, where the spectrum is covered by something like 0 and n where 0 is ‘the worst’ and n is ‘the fairest’. Moreover, it also says that this n must be unique. An analogue specification is done in ‘the most civilized portion of mankind’, where it is assumed that ‘mankind’ is a set within which there is a subset ‘(those) civilized’, which is also ordered (introduced by ‘the most’) in such a way that ‘the empire of Rome’ included the unique subset ‘the most civilized’. Interestingly, there is a sense in which the order must be given to subsets but not to their elements, meaning that there are different ‘civilized-types’ within ‘mankind’ but within a given subset of ‘civilized-types’ the items are not necessarily ordered (here the natural language allows both solutions, but there is no way in this case to understand which truth condition applies).
This can be represented by the following graph:

Graph 1
One of the remarkable features of [Graph 1] is that it shows how natural language is able to render simultaneously several features of reality that are not obviously related. In fact, in this regard, natural language is unmatched in allowing complicated relations and connections vis a vis other types of representations such as a video or a picture.[33] Here ‘simultaneously’ must be taken very seriously as a time indicator. In fact, as Noam Chomsky argued, natural language is composed by a series of discrete components expressed in a finite sequential way.[34] But what this account does not show is how natural language is able to give a subsection of a model of reality where events, objects, whatever are given simultaneously. In fact, [2] introduces first the ‘portion of the earth’ and then ‘portion of mankind’, but the reader clearly understands immediately that those features of the ‘empire of Rome’ are simultaneous. There is no perception of different timestamps over the two features, because the introduction of ‘In the second century…’ is immediately understood as applied to both sides of the ‘and’. As a result, although presented differently in the ‘finite sequence of words’, the proposition is understood independently on how it is uttered or read.
Before concluding, it will be worthwhile considering an example where complicated functions and sets of curious objects are introduced. Before jumping into this last section, I remark that what strikes (me) in this last analysis is the impressive level of efficiency of natural language in its ability to exert an impressive amount of work on apparently very tiny portions of the overall expressions and, specifically, by the ‘in’, ‘of’, and especially ‘and’. For instance, as analyzed, ‘and’ is fruitfully able to perform a merely Boolean operation and, at the same time, to reduce the number of words to convey the message effectively. In [1] we saw even a different function of ‘and’, where it was connecting simultaneously different objects and performing a Boolean operation at the same time. We know that ‘and’ can be even capable of more work!
For instance, ‘I plan to eat and go to the gym’ the ‘and’ is typically used as a time direction where ‘eating’ will come before ‘going to the gym’. Again, the implicit work done by the mind to deconstruct the correct message is impressive, but it is as impressive as the power of natural language to perform so much work with so little computational effort, at least not compared to what would be required to do the actual work in [SK3 & SK4].[35] This reminds me of Wittgenstein consideration about the resemblance between natural language and an organ: the heart is a pump but it is also a thermostat simultaneously. There is no way to understand the work of the heart and its importance in the economy of health without understanding all its functions simultaneously and distinctively. The same applies to natural language portions, which seems to be an incredible result of some sort of selection whose chance cannot be entirely reduced to a statistical trial-and-error approach. There is something we are missing altogether about it, and it is probably why for so long it was considered the way in which God created the world in so many religions: natural language baffles us and it keeps doing it. But we also know it is not a God-like thing as far as it has its own limits of expressions.[36]
Deconstructing a proposition with subjects, evaluations and beliefs
So far, we dealt with propositions about the world with only entities defined as objects and geospatial or geometrical relations with or without time. In this regard, although clumsily, set theory was able to cope with the task. Already noticeable were the many assumptions that would have immediately faced a fully philosophical dispute on metaphysical perspectives. However, at least prima facie, set theory and logics proved their worth behind the scenes of the curtain of natural language. However, we did not face any subjective statement, evaluation or whatever it intersects the world of the mind and the extension. This is an altogether different level of complication, as it should be clear once the analysis is done. To see the difference, I invite the reader to try him-herself.
[3] Caesar, being convinced that his lenity was known to all men, (…) resolved to deter others by inflicting an exemplary punishment on these.
This sentence is from another historical source, Julius Caesar in De Bello Gallico and one of my favorite passages.[37] Let’s see the break down.
[SK5] Start
[3.0] Assuming
[3.0.1] the existence of the set of all men,
[3.0.2] the existence of the set of actions,
[3.0.2.1] the set of actions can be specified to include only those performed by the items of the set [3.0.1],
[3.0.2.2] the set of actions can be specified to include the subset of ‘punishments’,
[3.0.3] the existence of the set of dispositional beliefs,
[3.0.3.1] the set of dispositional beliefs can be specified such to have a subset ‘resolutions’,
[3.0.3.2] dispositional beliefs can be intended as a relation between the set of men and the set of actions such that if an item (man) is given, then an action is also given,
[3.0.4] there is a relation between the set of dispositional beliefs and the set of actions such that R(b,a) for an item b of the of the set of dispositional beliefs and an item a of the set of actions,
[3.0.5] the set of knowledge is a subset of the set of beliefs such that there is a relation between the set of ‘knowledge’ and the sets of ‘actions’, ‘subjects’, ‘physical objects’, ‘social objects’ such that if an item of the set of men has a set of knowledge-belief that associate it to any of those to which ‘knowledge’ is associated to through established relations,
[3.1] There is a unique individual of the set of all men ‘Caesar’,
[3.2] The set of all men can be specified under the property ‘lenity’,
[3.3] For all the items of the set of all men, taken a single entity of it, it can be specified the property ‘knowledge’,
[3.4] There is a function whose domain is ‘knowledge’ and whose argument is ‘lenity’ such that for each item of the set of all men it can be associated ‘lenity’ through the ‘knowledge’ function.
[3.5] The unique individual ‘Caesar’ is associated to the dispositional belief ‘resolved’ that is associated to ‘deter’, which establishes a relation with ‘Caesar’ and ‘others (men)’.
[3.6] The set of punishment is partitioned so to include only ‘exemplary punishments’,
[3.7] There is a relation between ‘Caesar’ and ‘punishment’ established by the relation ‘deter’ applied to the set of ‘men’.
[SK5] End
As short and simple as it looks, [3] is extremely difficult to reduce to pure set theoretical description. What it says is essentially that a given individual of the set of men (‘Caesar’) whose subset of set of dispositional belief includes ‘deterrence’ among them. ‘Deterrence’ is a subset of the set of actions such that once such an action is given, then another belief is created in the set of beliefs of the men. The action of deterrence is paired with the punishment, which is also a subset of the set of actions. All this is under the condition that Caesar is simultaneously holding the belief that all the men to be punished for being deterred believe him to be a good person.
I must admit that I didn’t select this sentence for any other reason than for its stickiness to my mind and it took me by surprise on how difficult it is to fully disentangle it: its set theoretical architecture is extremely convoluted and involved multiple sets and multiple relations and functions among them. The reason should be immediately clear with the fact that we are dealing with a variety of different entities and their properties.
Once a rational subject is introduced, there is an entire plethora of assumptions that are introduced. At the very least, a ‘rational subject’ is an entity capable of actions through intentions.[38] Broadly speaking, a subject is anything that can translate beliefs into action. Hence, its essence is distributed between beliefs and actions. Beliefs are a way to intend the metal and cognitive domain, where actions deal with ‘reality’ or what can be defined as ‘extended’, in more classical terminology. It does not matter that there are strange people who believe that ‘there is only matter’ (whatever this curious sentence could mean).[39]
Natural language still reproduces the subject and his/her life in a quite different way than objects and actions. However, as it is clear, beliefs and actions are related, because beliefs’ content is about accepting or rejecting states of affair, evaluating them, or simply recognize them etc..[40] Even more complicated is the actions that are related to a given belief as origin, but they are intended to effect others’ beliefs, such as in the case of [3]. The many difficulties of [3] are due to the impressive diversity of combinations between beliefs, subjects’ attitudes and the rest of the universe. For instance, it is particularly difficult to get the ‘resolved to deter’ right because both ‘resolve’ and ‘deter’ are two dispositional beliefs where the first (‘resolve’) has its object in ‘deter’, which is another disposition, whose object is an action ‘inflicting’ explicated in the object of another set ‘punishment’ to be directed toward another set ‘all men’. In fact, the main sentence is expressing a disposition about a disposition toward a certain action that will have a certain disposition by those who will receive it! Let’s go back to the full proposition:
[3] Caesar, being convinced that his lenity was known to all men, (…) resolved to deter others by inflicting an exemplary punishment on these.
All this work is already impressively convoluted, but it is very compact. As it should be clear from [SK5], the conditions to understand [3] are quite significant in number and complexity.[41] First, there is an identification of a specific item of the set of all men ‘Caesar’ through a proper name. ‘being convinced’ is a way to avoid the formulation of an independent sentence such as ‘Caesar was convinced…’. The shortcut works asking to the reader to keep the information in the memory, and it acts as a specification over what ‘Caesar’ is assumed to believe ‘his lenity was known to all men’. This last bit does a lot of work in a very short space. It is saying that for each one item of the set of ‘all men’ is associated a special belief qualified as ‘knowledge’ (‘was known’), which has ‘his lenity’ as object. Notably, ‘his lenity’ is both the object of ‘Casar being convinced’ and ‘was known to all men’. ‘his’ is creating an attribution over Caesar’s properties such that ‘lenity’ is both assumed by Caesar to be one of his features and, at the same time, that the proposition ‘Caesar is good and nice’ is among the beliefs of ‘all men’. It is beyond saying that all these very complicated specifications are elegantly solved in a very short space in the natural language.
Then, the proposition goes on specifying another type of belief attributed to Caesar, ‘resolved’ and immediately specified by the ‘to’, so restricting the set of ‘resolution-dispositional beliefs’ over one specifically ‘deter’. However, as any dispositional belief requires an object (we can even intend a belief as a function where the domain is given by what the subject thinks and co-domain what he/she thinks about), this is specified by ‘others’. ‘by inflicting’ is operating back to ‘deter’, restricting specifically the nature of the intention ‘deter’ (but not ‘resolve’). Finally, it states that this restriction (‘by inflicting’) is explicated through a specific item of the set of ‘punishments’ as the ‘exemplary’. Here the most remarkable components of the proposition are the impressive work done by ‘being convinced… to all men’ and ‘resolve to deter by inflicting’ as to fully understand all the underneath truth conditions require an impressive amount of work that, again, are all included in an extremely short space.
Conclusions – Set theory, formal and informal logic and deep textual analysis
The three different sentences we considered were analyzed mainly through set theoretical language and set theory axioms and schemata behind the scenes.[42] Notably, a tedious philosopher could observe that predicative first order formal logic was not used if not in very limited ways. The reason is simple. We tried to dispel the love for propositions and their truth-value. The focus was on how natural language manages to describe entire portions of reality in a very compact, efficient way. The goal was indeed to step back from the traditional propositional focus toward the components never losing sights toward what matters: how the combination of different components of natural language merge together to give back portions of models of reality.
As the focus is on specific propositions, we did not model arguments but its building blocks. Frankly, modelling arguments should be much more straightforward, although there is a different level of complexity as relations among different propositions are involved and natural language resolve it in many ways shortcutting logical passages and connectives as already seen (which is also the base of complaints from the clever logicians).[43] However, some work was already done in this direction and probably will be done in the future.[44]
For the moment, instead, I will conclude with two considerations which hopefully will be expanded at some point. The first is about the impressive expressivity of natural language, and its incredible capacity to exert so much work on very tiny pieces of expressions (e.g. the ‘of’ and ‘by’ or ‘and’ so far considered). There is a clear sense in which there is a disproportion between the sheer length of portion of the language and their capacity to express meanings, being it connections, spatial or temporal relations, functions, or general relations. Secondly, natural language appears incredibly capable in describing and improving its expressivity over very different types of portions of reality. As seen, in principle everything expressed in set theoretical terms can also be expressed by natural language but not vice versa. This leads me to the conclusion that anything formal can be somehow expressed by natural language in the first place, suggesting the fact that natural language is a sort of ‘coding library’ from which we can operate restriction for different logical or mathematical purposes. If so, then natural language should be much more revered from a merely formal perspective, as it is the library from which we specify sub-coding pieces of more precise work.
Natural language is not perfect, as we need precision tools to improve our capacity to describe and ultimately understand reality, from one side, and it allows logical fallacies, vagueness, imprecisions and semantic mistakes, from another side. However, what is really important is that we can reset natural language to follow more precise rules of logics and set theory, when we really need it, and natural language would gently comply. Ultimately, if natural language is the place where everything that can be said and understood can be expressed, then it must be admired for its incredible capacity and any misuse is not its fault as much as it is not any brain misfunction its misuse: it is on us, and not on our brain, what we do with it. And as much as we love to discharge responsibility, there is no way to escape the fact that natural language has nothing wrong, providing it is used properly.
[1] See Pili, G., ‘Epicuro,’ Scuola Filosofica, 2011.
[2] Mittelstrass, J. (1979). ‘The Philosopher’s conception of Mathesis Universalis from Descartes to Leibniz.’ Annals of Science, 36(6), 593–610. https://doi.org/10.1080/00033797900200401
[3] There is a sense in which they can, but they were not first intended to be disjointed in a fundamental sense.
[4] There are infinite bad formulations of naïve set theory and ZFC, I stick with one of the few that I personally like: Schimmerling, E., (2011), A course on set theory, Cambridge:Cambridge University Press, and the classic Halmos, P.R., 1960. Naive set theory. van Nostrand.
[5] Although this statement could be controversial, I still believe it holds perfectly. This is essentially the untold story when learning a formal language for the first time. In fact, it is also a major matter of confusion for those that are naively exposed to formal logic alone early on. In fact, I do believe, the confusion remains in many ‘thinkers’ in later developments bringing to the paradoxical conclusion that if people were confused by the tricks of natural language, nowadays ‘people’ – namely, philosophers – are confused by formal logics and set theory among many other things. I let the reader decide who is more confuse and what confusion is better! One thing is clear, though. Confusion of any sort is an unhealthy situation and ‘logical confusion’ is no better only because we draw stranger signs into a black board with the only achievement to let any other believe that we know and they don’t.
[6] Whitehead, A.N. and Russell, B., (1927), Principia mathematica. Cambridge: Cambridge University Press.
[7] Although, it must be said, it would have been something it would have been in my tastes, if only I had one hundred years less.
[8] For instance, when the rule of negation is given in the Principia Mathematica there more natural language than anything else, including the ‘definition of negation’.
[9] See Pili, G., (2017), ‘Le ricerche filosofiche e il secondo Wittgenstein’, Scuola Filosofica, https://www.scuolafilosofica.com/5810/le-ricerche-filosofiche-secondo-wittgenstein
[10] Pili, G., (2017), ‘Le ricerche filosofiche e il secondo Wittgenstein’, Scuola Filosofica, https://www.scuolafilosofica.com/5810/le-ricerche-filosofiche-secondo-wittgenstein
[11] There are infinite amounts of bad accounts of Gödel’s proof(s). Here I reference Gödel, K., 1986. Kurt Gödel: collected works: volume I: publications 1929-1936 (Vol. 1). Oxford University Press, USA, Pili, G., (2015), ‘Cosa ne pensava davvero Kurt Gödel?’, Scuola Filosofica, https://www.scuolafilosofica.com/4831/cosa-ne-pensava-davvero-kurt-godel, Gödel K., (1944), “La logica matematica di Russell”, in Gödel K., (1995), Scritti scelti, Bollati Boringhieri, Milano.
[12] Notably, to achieve this relatively ‘simple’ capacity of natural language (reflexivity etc.), it took an enormous amount of technical work. However, the technical aspects of Godel’s masterpiece found a good use as it led to the discovery that there is a way to rewrite arithmetic in logical terms and logical terms in arithmetical terms. Essentially, as Descartes understood that geometry and numbers are two sides of the same coin, allowing problem solving in both sides and so multiplying the capacity to solve mathematical problems in geometrical terms and vice versa, so Godel allowed a new understanding of the powerful relation between numbers and logical propositions and vice versa. It is one of the most remarkable human achievements. The remarkability of the achievement was cleverly explored by Hofstadter, D. R. (1999). Gödel, Escher, Bach: an eternal golden braid. Basic books.
[13] In fact, we should take this suggestion from logic seriously than we actually do and disregarding more noise in our lives!
[14] In fact, I don’t know how a mathematical question can be even formulated without being it expressed in natural language.
[15] But this must have been how Godel himself see the problem: Gödel K., (1951), “Alcuni teoremi basilari sui fondamenti della matematica e le loro implicazioni filosofiche”, in Gödel K., (1995), Scritti scelti, Bollati Boringhieri, Milano. For a general commentary: Pili, G., (2015), ‘Cosa ne pensava davvero Kurt Gödel?’, Scuola Filosofica, https://www.scuolafilosofica.com/4831/cosa-ne-pensava-davvero-kurt-godel
[16] However, there must be something that establish what the domain of interpretation is and connects the language to the new domain.
[17] See Pili, G., (2014),‘Filosofia del linguaggio – Approcci possibili alle teorie della verità, Scuola Filosofica, https://www.scuolafilosofica.com/3540/filosofia-del-linguaggio-approcci-possibili-alla-teoria-della-verita
[18] I will give a full proof of this point later on.
[19] Wittgenstein L., (1921), Tractatus Logico-Philosophicus, Chiron Academic Press, Sweden.
[20] Ibid.
[21] Obviously, this is a very dry conception of science, which does not allow any meaningful conversation on scientific bases on the nature of the universe or time, a major sport of many physicists – but this is all beyond our purposes.
[22] If anything can be clear. According to discussion of relatively forgotten Italian philosophers still alive – I think, Wittgenstein vision of what is an object, state of affairs and facts are quite controversial and, basically, unfollowed by successive philosophers. I always found at ease in those notions, providing that one does not take them as seriously as those do. But one of the lessons about anything in philosophy is that nothing that is pretended to be as serious can stand, as reality is too big to be cheaply contained in words. What it matters is that intuitively Wittgenstein’s basic metaphysics is quite handy for understanding the world.
[23] Wittgenstein L., (1953), Philosophical Investigations, McMillan, New York, see Pili, G., (2017), ‘Le ricerche filosofiche e il secondo Wittgenstein, Scuola Filosofica, https://www.scuolafilosofica.com/5810/le-ricerche-filosofiche-secondo-wittgenstein
[24] Wittgenstein L., (1939), Lezioni sui fondamenti della matematica, Bollatti-Boringhieri, Milano.
[25] Yes, I am not alone and maybe you too: Harrison, J., “Formal proof—theory and practice.” Notices of the AMS 55, no. 11 (2008): 1395-1406.
[26] Pili, G., ‘La storia come libera creazione delle verità eterne’, Scuola Filosofica, 2017, https://www.scuolafilosofica.com/5915/5915
[27] See Schimmerling, E., (2011), A course on set theory, Cambridge:Cambridge University Press.
[28] This is due to the fact that ‘is’ here is both used as ‘property attributor’ and as ‘locator’ (in the use such as ‘it is (placed) here’.
[29] Here I am considering ‘Christian Aera’ for obviously what it is: a convention, exactly in the same way I am considering ‘centuries’ as a convention. The sheer fact that ‘Christian Aera’ and ‘centuries’ are somehow related to reality (in quite different way!) does not change the fact that they stand for conventions on how to measure the common time-flow for coordinating purpose. For a better analysis of time, see Pili, G., (2024), ‘A Pluralistic Understanding of Time – Time as Eternal truths’, Scuola Filosofica, https://www.scuolafilosofica.com/11906/a-pluralistic-understanding-of-time#_ftn1
[30] I jus tried a prompt in Chat-GPT4 and the result is ludicrous.
[31] Searle, J., The construction of social reality. Simon and Schuster, 1995.
[32] See for more on this point below.
[33] For instance, it would be arguably very difficult to depict [2] and as a proof of a concept, the soon better-than-whatever AI, in its free and cheap version called ‘DeepAI.Org’ was very able to depict a series of mediocrities whose understanding would require an effort that I am fairly unwilling to make.
[34] See Pili, G., (2011), ‘Noam Chomsky – Vita e Grammatica Generativa’, Scuola Filosofica, https://www.scuolafilosofica.com/558/noam-chomsky, Chomsky N., ‘Three models for the description of language.’ www.chomsky.info.
[35] Here I interject a criticism I received by an old friend of mine many years ago, who pointed out that we don’t actually know how much work is actually exerted by the brain when we think about these kinds of operations, as the computations can be done under the conscience level. That’s definitely the case for the brain’s operations at a electrochemical level. However, as I am still convinced enough that the mind does operate as a software in comparison to the hardware, there is a clear sense in which, whatever the brain is doing, the actual software-level computation exerted by the mind is essentially minimal. This would be similar to simple typing in ‘Word’in a PC: I don’t know how the simulation of the writing is made electronically, but the actual operation in ‘Word’ is minimal in comparison with a geospatial calculation over a given dataset. I can see that a better defence can be made over the opposite proposition, and I also share the idea that the brain does a lot of work in many senses. I just cannot buy the concept that to understand a single sentence the brain is actually computing all its set theoretical and logical ramification.
[36] Once I was listening to a dear colleague of mine talking about the fact that ‘natural language is limitlessly expressively powerful.’ Then I realised that this is another instance of the ‘lack of friction’ or ‘idealised’ bias. As war tend to the ‘absolute’ under untested reasoning and lack of proper reality according to Clausewitz, so natural language seems essentially unboundedly powerful in its expression. However, there are several things that natural language cannot do. For instance, it cannot disambiguate itself in the same time in which a given sentence is pronounced. As an example: ‘The tank leaks oil’ can mean that there is a tank (cistern) that contains a fluid ([olive] oil) and it is leaking. However, it can also mean that a given military vehicle is leaking oil (petroleum). Natural language can fix the problem only clarifying through other words what is the intended meaning (that is, giving more explicit rules of interpretation). Moreover, this clarification shows how natural language can make sense only assuming the existence of an external referee that, one way or another, can go outside what stated and check. In fact, without this external intervention, natural language would lack the capacity to anchor itself to anything else than empty words (these kinds of problems arise when confrontations over words arise such as in a family discussion, broken relation etc., where the ‘trust’ on the ‘words’ is suspended. For a much more dramatic case, see Pili, G., Filosofia Pura della Guerra, Rome(Ita): Aracne, Chap. 17). The limitations of expressivity of natural language would bring us too far, but it was important to show that natural language, as powerful as its, it is exactly as anything else: imperfect.
[37] It is particularly fascinating the fact that analysing these texts from different centuries shows the fact that natural language was already as rich back then, which shows indirectly how the mind of those people must have been capable of reasoning as much as us, at least in theory. In fact, the metaphysical and linguistic architecture behind the scenes must have been already in place at the time as, otherwise, those statements would have been unthinkable (literally).
[38] For a possible set theoretical and logical reduction of the rational subject see Pili, G., Filosofia pura della Guerra, Rome:Aracne, Chap. 5, based on Pili, G., (unpublished), ‘Teoria della societa’ su basi matematiche elementari’.
[39] These kinds of metaphysical statements are those that help in discrediting philosophy (and those who try to express it) in their unilateral reductionism and, as such, can be only compared to religious analogues (here intended as non-philosophical in nature). For considerations about this point and beyond see Pili, G., (2023), ‘Life as an Open-Ended act of Creation – Or Why Life is Unsolvable’, Scuola Filosofica, https://www.scuolafilosofica.com/11416/why-life-is-unsolvable
[40] Actions are a subset of the set of the state of affairs. Their nature is factual and, essentially, reducible to relations among objects. It is a matter of convenience that we disjoint ‘actions’ from ‘factual changes’ or any physical change of distribution of objects, as ‘actions’ are usually intended as the result of intentions. Hence, an ‘action’ is a fact whose cause is an intention in a relevant sense. However, again, we are introducing here many terms that are advocating for a metaphysical understanding of the world (e.g. we are assuming the existence of intentions as if they can be comparable to actions as, somehow, intentions have to be causally related to actions to make the work possible). It is clear that this is not the place to solve or debate these kinds of issues, but this is another place where set theory can reduce, but not exhaust, natural language and all its metaphysical hurdles.
[41] Here I like the word ‘complexity’ exactly because the net of connections between different types and levels of meanings is such that the word seems to be more appropriate that just ‘convoluted’.
[42] It would have taken too long going through why the reduction was given in that way, what axioms are grounding the reduction etc. I focused my attention only on the jump between an informal naïve set theory approach expressed in a semi-formalised way and a properly formalised formulation. There is neither space nor reason for going beyond this level given that the object of the analysis is natural language and not how set theory work. Any logician, philosopher or mathematician is invited to go deeper into the work – if any will ever read it.
[43] Exactly because of these features of natural language, the large language models are able to perform in the way they do thanks to statistical properties associated to words, plus a plethora of superpositions into the possible results (maybe it is the way they locally resolve issues related to grammar and syntax). In addition, it could be the reason why they are so weak in general reasoning. We will see how capable they will be after innovations in the reasoning area.
[44] See Pili, G., (2017), ‘Il ragionamento umano e le sue differenze con il ragionamento formale’, Scuola Filosofica, https://www.scuolafilosofica.com/6026/6026




Be First to Comment